Revision

Back to NLP

Introduction

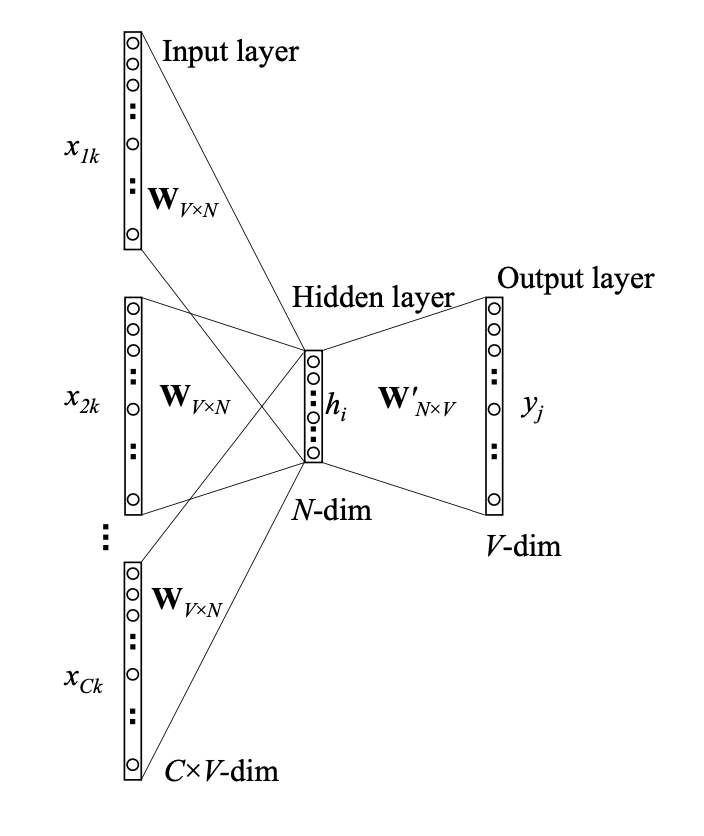
Word2Vec is an unsupervised method to generate vector representations of words. Once each word is assigned to an ID, a dictionary or a one-hot matrix representation is used to map every word to its vector representation.

This vector representations of words are computed such as similar words have similar representations.

CBOW

CBOW for Continuous Bag of Word predicts a word given context, ie it tries to predict a word given surrounding words in a given window:

Where:

\(x_{i,k} := w_i\) represent the one hot encoding of the \(i\)-th word of the context which is 0 everywhere except for index \(k\),
\(x_{1,k}, \ldots, x_{C,k}\) represent the one hot encoding of the \(C\) surrounding context words,
\(y_j\) represents the probability to predict word \(j\) given the context,
\(W_{V \times N}\) is a matrix of weights that encodes the context words to vector representation,
\(W_{N \times V}\) is another matrix of weights that encodes the tested central words to vector representations.
\(V\) is the size of the vocabulary,
\(N\) is the size of the vector representation (hyperparameter),
The hidden layer \(h\) contains the representation of the context words.

The two matrix \(W_{V \times N}\) and \(W_{N \times V}\) are different even if they have a similar meaning.

Also note that word with ID \(x_i\) will have as context representation \(W_{V \times N}(x_i)\) and as central word representation \(W_{N \times V}(x_i)\).

The hidden layer \(h\) is an average of the representation of each context word ie:

\[\begin{eqnarray} h &&= \frac{1}{C} (W_{V \times N})^T (x_1 + x_2 + \ldots + x_C) \\ h &&= \frac{1}{C} (v_{w_1} + v_{w_2} + \ldots + v_{w_C})^T \end{eqnarray}\]

Where:

\(v_{w_i}\) represent the context representation of word \(x_i\)

The probability of word \(w_j\) given context is then:

\[\begin{eqnarray} p(w_j \vert (w_{j-c/2}, \ldots, w_{j-1}, w_{j+1}, \ldots, w_{j+c/2})) && = p(w_j \vert h) \\ && = \frac{\exp((v'_{w_j})^T h)}{\sum_k^V \exp((v'_{w_k})^T h)} \\ && = \frac{\exp(u'_{w_j})}{\sum_k^V \exp(u'_{w_k})} \\ && = y_j \end{eqnarray}\]

Where:

\(v'_{w_i}\) represent the central word representation of word \(w_i\),
\(u'_{w_i} = (v'_{w_i})^T h\).

Optimization

The goal of the model is to maximize \(p(w_O \vert h)\):

\[\begin{eqnarray} p(w_O \vert h) &&= \max y_O \\ &&= \log y_O \\ &&= \log \frac{\exp((v'_{w_O})^T h)}{\sum_k^V \exp((v'_{w_k})^T h)} \\ &&= \log \exp((v'_{w_O})^T h) - \log \sum_k^V \exp((v'_{w_k})^T h)\\ &&= (v'_{w_O})^T h - \log \sum_k^V \exp((v'_{w_k})^T h)\\ &&= u'_{w_O} - \log \sum_k^V \exp(u'_{w_k}) := E \end{eqnarray}\]

Where:

\(E = -\log p(w_O \vert h)\) is the loss function to minimize.

We will use Gradient Descent to minimize \(E\). The derivative of \(E\) with respect to \(u_j\) is:

\[\begin{eqnarray} \frac{dE}{du_j} &&= \frac{d}{du_j} -\log(w_O \vert h) \\ &&= -\log \sum_k^V \exp(u'_{w_k}) - u'_{w_O} \\ &&= \exp(u'_{w_j}) \frac{1}{\sum_k^V \exp(u'_{w_k})} - \frac{u'_{w_O}}{du_j} \\ &&= y_j - t_j := e_j \end{eqnarray}\]

Where:

\(t_j = \mathrm{1}_{j=O}\) is 1 when \(w_j\) is the actual output word \(w_O\), otherwise \(t_j = 0\).

The derivative with respect to \(v'_{w_j}\), the central vector word representation of word \(w_j\) is then

\[\begin{eqnarray} \frac{dE}{dw_j} &&= \frac{dE}{du_j} \frac{du_j}{dv'_{w_j}} \\ &&= e_j \frac{d}{dv'_{w_j}}(v'_{w_j})^T h \\ &&= e_j \cdot h \end{eqnarray}\]

The Gradient Descent update rule for central word representation of word \(w'_j\) (hidden -> output) is then:

\[(v'_{w_j})^{(new)} = (v'_{w_j})^{(old)} - \alpha \cdot e_j \cdot h\]

For context word we have:

\[\begin{eqnarray} \frac{dE}{dh} &&= \sum_{j=1}^V \frac{dE}{du_j} \frac{du_j}{dh} \\ &&= \sum_{j=1}^V e_j w'_j := EH \\ \end{eqnarray}\]

Intuitively, since vector EH is the sum of output vectors of all words in vocabulary weighted by their prediction error \(e_j = y_j − t_j\), we can understand the above equation as adding a portion of every output vector in vocabulary to the input vector of the context word. If, in the output layer, the probability of a word \(w_j\) being the output word is overestimated (\(y_j \gt t_j\)), then the input vector of the context word \(w_I\) will tend to move farther away from the output vector of \(w_j\); conversely if the probability of \(w_j\) being the output word is underestimated (\(y_j \lt t_j\)), then the input vector wI will tend to move closer to the output vector of \(w_j\); if the probability of \(w_j\) is fairly accurately predicted, then it will have little effect on the movement of the input vector of \(w_I\).

And:

\[\begin{eqnarray} \frac{dE}{dw_k} &&= \frac{dE}{dh} \frac{dh}{dw_k}\\ &&= EH \cdot w_k\\ \end{eqnarray}\]

\(w_k\) is just a one-hot vector having a 1 on its \(k\)-th row.

The the update rule for context word representations (input -> hidden) is then:

\[(v_{w_{I,c}})^{(new)} = (v_{w_{I,c}})^{(old)} - \frac{1}{C} \alpha \cdot EH^T \;\;\;\; \text{for } c \in \{1, \ldots, C\}\]

Only the weights of input words \((I, c)\) from the context are updated.

Skip-gram

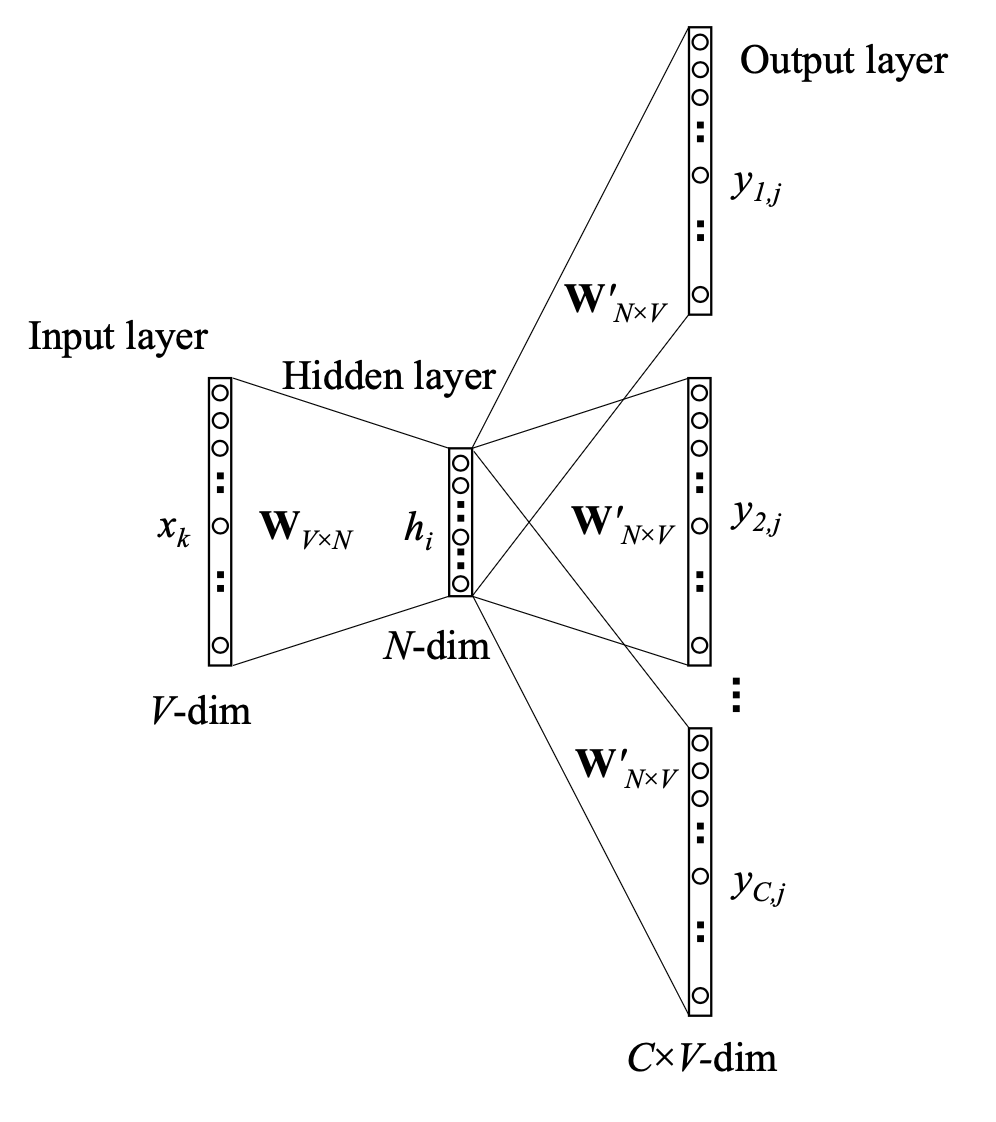
Skip-gram model predicts context words given the central word ie it tries to predict context words in a window given the central word:

Where:

\(x_k\) represent the central word,
\(y_{i,j}\) represents the probability to predict word \(j\) as context word \(i\),
\(W_{V \times N}\) is a matrix of weights that encodes the context words to vector representation,
\(W_{N \times V}\) is another matrix of weights that encodes the tested central words to vector representations.
\(V\) is the size of the vocabulary,
\(N\) is the size of the vector representation (hyperparameter),
The hidden layer \(h\) contains the representation of the central word.

The two matrix \(W_{V \times N}\) and \(W_{N \times V}\) are different even if they have a similar meaning.

Also note that word with ID \(x_i\) will have as central word representation \(W_{V \times N}(x_i)\) and as context word representation \(W_{N \times V}(x_i)\).

The hidden layer \(h\) is:

\[h = (W_{V \times N})^T x_k = v_{x_k}\]

The probability of \(c\)-th word of the context being word \(j\), \(w_{c,j}\) given central word \(w_I\) is then:

\[\begin{eqnarray} p(w_{c,j} \vert w_I) && = p(w_j \vert h) \\ && = \frac{\exp((v'_{w_{c,j}})^T h)}{\sum_k^V \exp((v'_{w_{c,k}})^T h)} \\ && = \frac{\exp(u'_{w_{c,j}})}{\sum_k^V \exp(u'_{w_{c,k}})} \\ && = y_j \end{eqnarray}\]

Where:

\(v'_{w_i}\) represent the central word representation of word \(w_i\),
\(u'_{w_i} = (v'_{w_i})^T h\).

Where:

\(v'_{w_i}\) represent the central word representation of word \(w_i\).

Optimization

The goal of the model is to maximize \(p((w_{1,O}, \ldots, w_{C,O}) \vert h)\):

\[\begin{eqnarray} p((w_{1,O}, \ldots, w_{C,O}) \vert h) &&= \max \prod_{i=1}^C y_i \\ &&= \prod_{c=1}^C \frac{\exp((v'_{w_{c,O}})^T h)}{\sum_k^V \exp((v'_{w_k})^T h)} \\ &&= \prod_{c=1}^C \frac{\exp(u'_{w_{c,O}})}{\sum_k^V \exp(u'_{w_k})} \\ &&= \log \prod_{c=1}^C \frac{\exp(u'_{w_{c,O}})}{\sum_k^V \exp(u'_{w_k})} \\ &&= \log \frac{1}{\sum_k^V \exp(u'_{w_k})} \prod_{c=1}^C \exp(u'_{w_{c,O}}) \\ &&= \sum_{i=1}^C \log \exp(u'_{w_{c,O}}) - \log \sum_k^V \exp(u'_{w_k}))\\ &&= \sum_{c=1}^C u'_{w_{c,O}} + C \cdot \log \sum_k^V \exp(u'_{w_k})) := -E \end{eqnarray}\]

Where:

\(E = -\log p((w_{1,O}, \ldots, w_{C,O}) \vert h)\) is the loss function to minimize.
\(u_{w_k}\) does not depend on the position of the context word \(c\) ie \(u_{w_{c,k}}=u_{w_k}\)

We will use Gradient Descent to minimize \(E\). The derivative of \(E\) with respect to \(u_j\) is:

\[\begin{eqnarray} \frac{dE}{du'_{c,j}} &&= \frac{d}{du'_{w_{c,j}}} -\log p((w_{1,O}, \ldots, w_{C,O}) \\ &&= \frac{d}{du'_{w_{c,j}}} \left[-\sum_{c=1}^C u'_{w_{c,O}} + C \cdot \log \sum_k^V \exp(u'_{w_k}))\right] \\ &&= C \cdot \frac{\exp(u'_{w_{c,j}}}{\sum_k^V \exp(u'_{w_k}))} - \frac{du'_{w_{c,O}}}{du'_{w_{c,j}}} \\ &&= y_{c,j} - t_{c,j} := e_{c,j} \end{eqnarray}\]

Where:

\(t_{c,j} = \mathrm{1}_{j=O}\) is 1 when \(w_{c,j}\) is the actual output word \(w'_{c,O}\), otherwise \(t_{c,j} = 0\).

The derivative with respect to \(v'_{w_{c,j}}\), the context vector word representation of word \(w'_{c,j}\) is then

\[\begin{eqnarray} \frac{dE}{dw'_j} &&= \sum_{c=1}^{C} \frac{dE}{du'_{w_{c,j}}} \frac{du'_{w_{c,j}}} {dv'_{w_j}} \\ &&= \sum_{c=1}^{C} e_{c,j} \cdot h := EI_j \cdot h \end{eqnarray}\]

Where:

\(EI_j := \sum_{c=1}^{C} e_{c,j}\).

The Gradient Descent update rule for context word representation of word \(w_j\) (hidden -> output) is then:

\[(v'_{w_j})^{(new)} = (v'_{w_j})^{(old)} - \alpha \cdot EI_j \cdot h \;\;\; \text{for } j \in \{1, \ldots, V\}\]

For the central word we have:

\[\begin{eqnarray} \frac{dE}{dh} &&= \sum_{j=1}^V \frac{dE}{du_j} \frac{du_j}{dh} \\ &&= \sum_{j=1}^V e_j w'_j := EH \\ \end{eqnarray}\]

And:

\[\begin{eqnarray} \frac{dE}{dw_k} &&= \frac{dE}{dh} \frac{dh}{dw_k}\\ &&= EH \cdot w_k\\ \end{eqnarray}\]

\(w_k\) is just a one-hot vector having a 1 on its \(k\)-th row.

The the update rule for central word representation (input -> hidden) is:

\[(v_{w_I})^{(new)} = (v_{w_I})^{(old)} - \alpha \cdot EH^T\]

Only the weights of the current central word are updated.

Hierarchical Softmax

To speed up the computation of the softmax function (that require to compute at each update of the parameters the constant \(\sum_k^V \exp(w_k)\)), one can use hierarchical softmax.

Hierarchical softmax computes the softmax using a tree representation:

See word2vec Parameter Learning Explained by Xin Rong for more informations.

Resources:

See: