The Vapnik� Chervonenkis dimension is a measure of the complexity of a class \(\mathcal{H}\) of models. Its definition is based on the notion of shattering.
A dataset \(D=\{x^{(1)}, \ldots, x^{(n)}\}\) of points \(x^{(i)}\) is shattered by hypothesis class \(\mathcal{H}\)� if and only if for any set of labels \(\{y^{(1)}, \ldots, y^{(n)}\}\), there exists some consistent classifier \(h\), i.e. a classifier \(h\) such that \(h(x^{(i)}) = y^{(i)} \forall i = 1, \ldots ,n\).
An hypothesis class \(\mathcal{H}\)� shatters \(D\) if whatever the labels \(y\), I could find a parametrization of a model \(h \in \mathcal{H}\) which would perfeclty labels all the samples.
The Vapnik–Chervonenkis (VC) dimension is a measure of the capacity (complexity) of a set of functions that can be learned by a statistical binary classification algorithm.
It is defined as the cardinality of the largest set of points that the algorithm can shatter, which means the algorithm can always learn a perfect classifier for any labeling of at least one configuration of those data points.
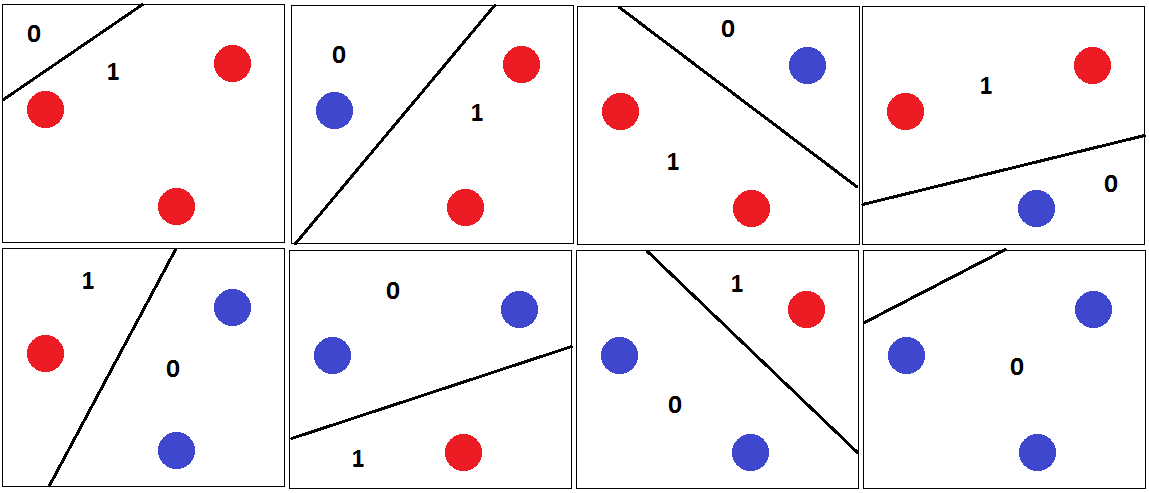
The class \(\mathcal{H}\) of linear models in dimension 2 has a VC dimension of 3, \(VC(\mathcal{H})=3\).
Indeed, any combination of labels \(\{y^{(1)}, y^{(2)}, y^{(3)}\}\) for the inputs \(\{x^{(1)}, x^{(2)}, x^{(3)}\}\) can be shattered by a well parametrized linear model \(h \in \mathcal{H}\) (in dimension 2):

However for any position of 4 samples \(\{x^{(1)}, x^{(2)}, x^{(3)}, x^{(4)}\}\) it is impossible to find a well parametrized linear \(h \in \mathcal{H}\) that would shattered any combination of the labels \(\{y^{(1)}, y^{(2)}, y^{(3)}, y^{(4)}\}\).
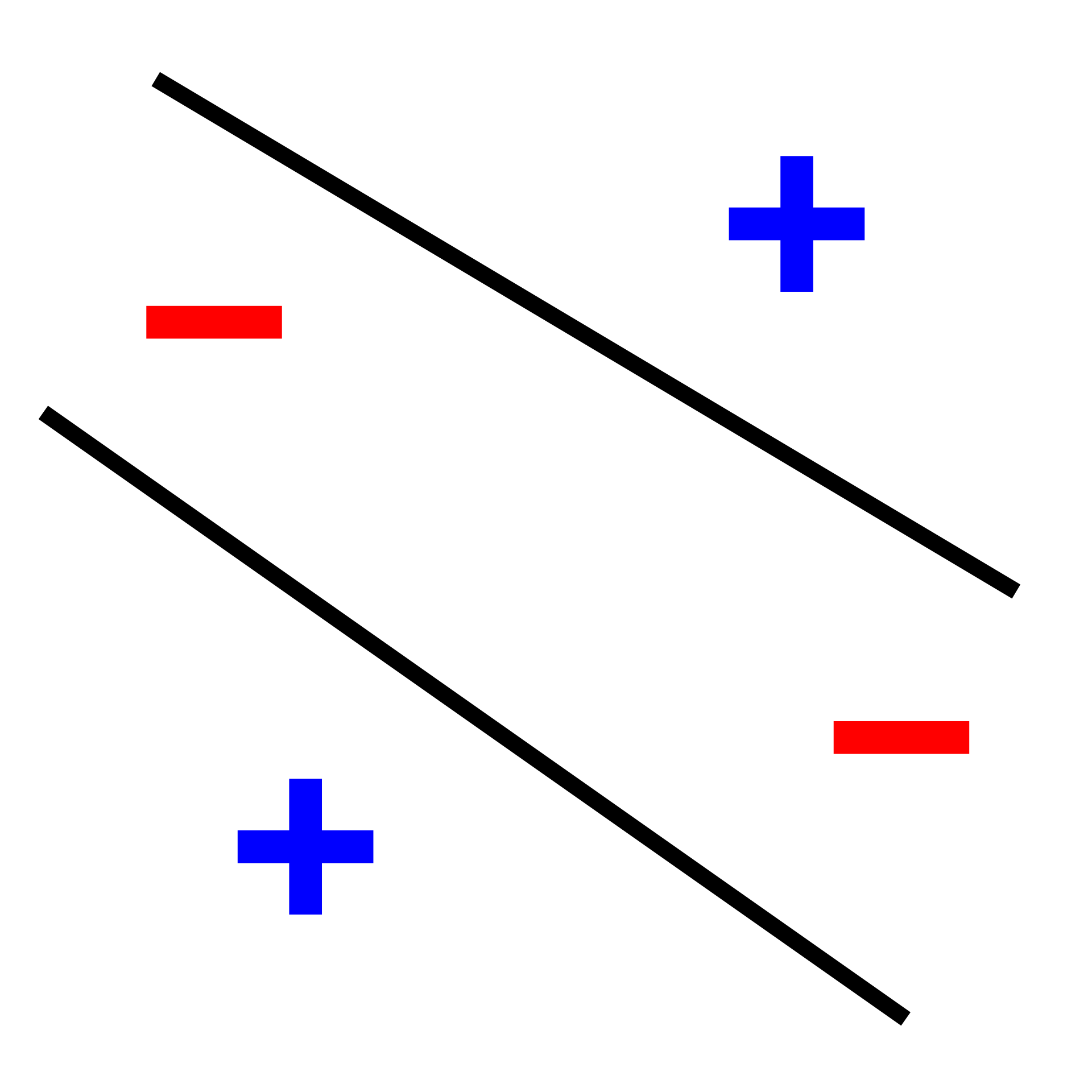
Here is a visual representation of 4 points \(\{x^{(1)}, x^{(2)}, x^{(3)}, x^{(4)}\}\) with labels \(\{y^{(1)}, y^{(2)}, y^{(3)}, y^{(4)}\}\) (blue plus and red scores) that can’t be shattered in dimension 2.
To show that hypothesis class \(\mathcal{H}\) has VC-dimension \(d\) in input space \(\chi\), consider this adversarial “shattering game”:
The VC-dimension of \(\mathcal{H}\) in \(\chi\) is the maximum \(d\) that we can choose so that we always succeed.
See: