The activation function is very important in a neural network. Without activation function, an ANN would be just a serie of linear regressions (which is equivalent to a single linear regression).
The non linear activation function allows the ANN to represent non linear output.
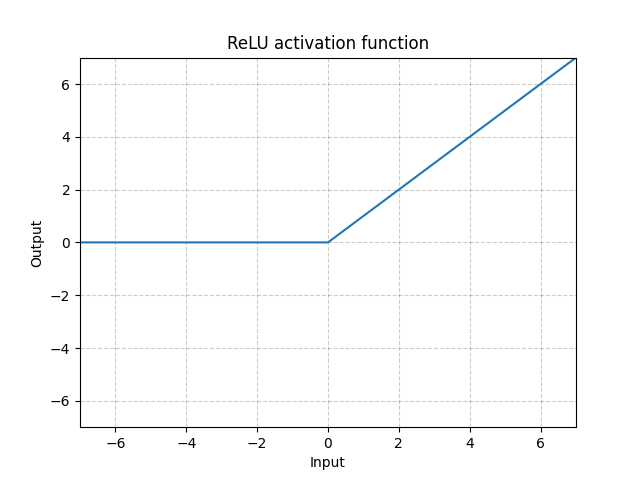
ReLU for Rectified Linear Unit is a commonly used activation function. It’s a really simple function.

\(ReLU\) works well in general but is prone to vanishing gradient.
Leaky ReLU (Rectified Linear Unit) is a little twick of the ReLU activation function.
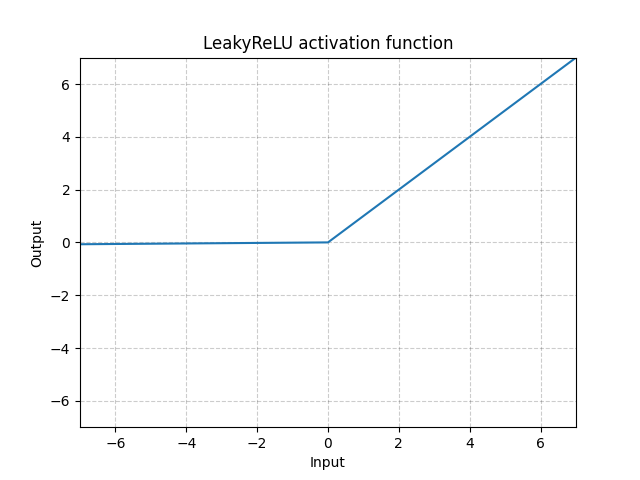
Leaky ReLU is not prone to vanishing gradient as the original ReLu activation function as it does not have a null gradient for negative values.
ELU (exponential linear unit) is another alternative to ReLU.

ELUis not prone to vanishing gradient as the original ReLu activation function as it does not have a null gradient for negative values.
SELU for Scaled Exponential Linear Unit is a self normalizing activation function. That means that this activation function preserves the mean and variance of its input.
It is particularly useful for network initialized with a gaussian distribution \(\mathcal{N}(0,1)\) as the activation function will preserve the normality all along.
It may be used with AlphaDropout which is a dropout method that also preserves the normality of the network.
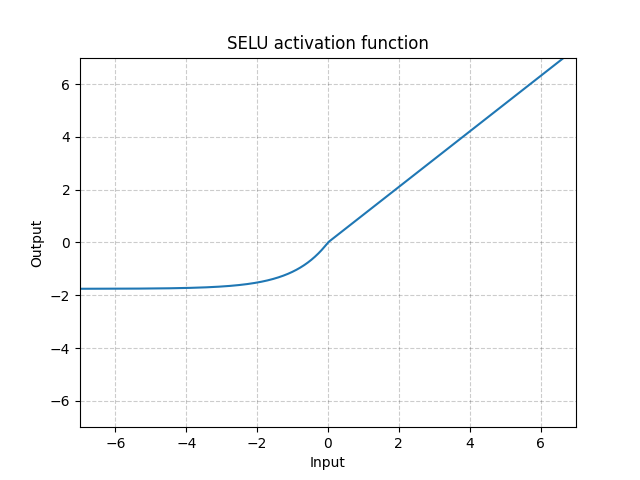
Where:
\(\lambda\) and \(\alpha\) have be computed by the author of the method in their paper.
Gaussian Error Linear Unit is an activation function that has been used in the Transformer models BERT and GPT-2.

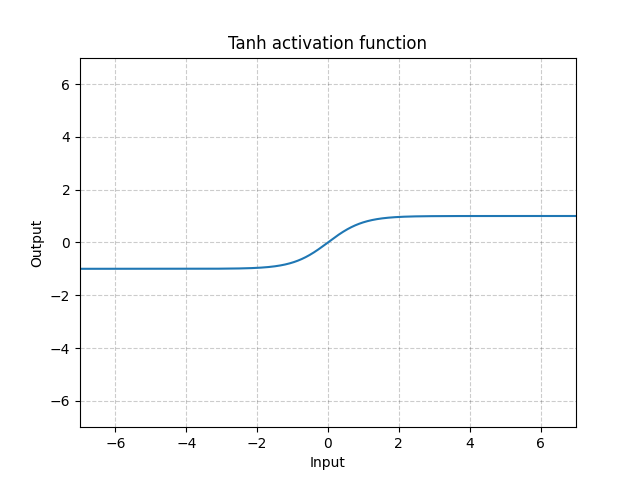
Tanh is another activation function but which is less used.
Sigmoid is another activation function but which is less used (it is widely used as an output function to map value between 0 and 1). See also Sigmoid in Logistic Regression.

See: