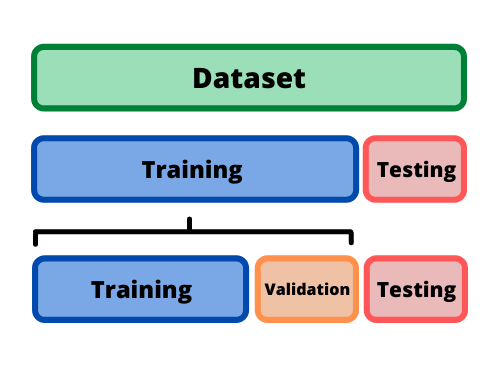
When training a model, 3 different set are needed, the train set to statistically estimates the parameters, the validation set to estimate the hyperparameter and the test set to test the model on unseen data.
Hence one needs to split its initial datset in 3 parts. This generates a loss of training data and some methods exist to avoid loosing precious data.

The split in done in two steps: first separate the test from the training data and then split the remaining training data in training (for statistical estimation) and validation (for estimation of hyperparameters).
Note than sometimes validation set is refered as test set.
Cross-validation, or out-of-sample testing, is a method for assessing how the results of a statistical analysis will generalize to an independent data set.
Cross-validations technics use different splits of train and validation sets in order to use each data sometimes for training and sometimes for validation. Note that test data always remains the same.
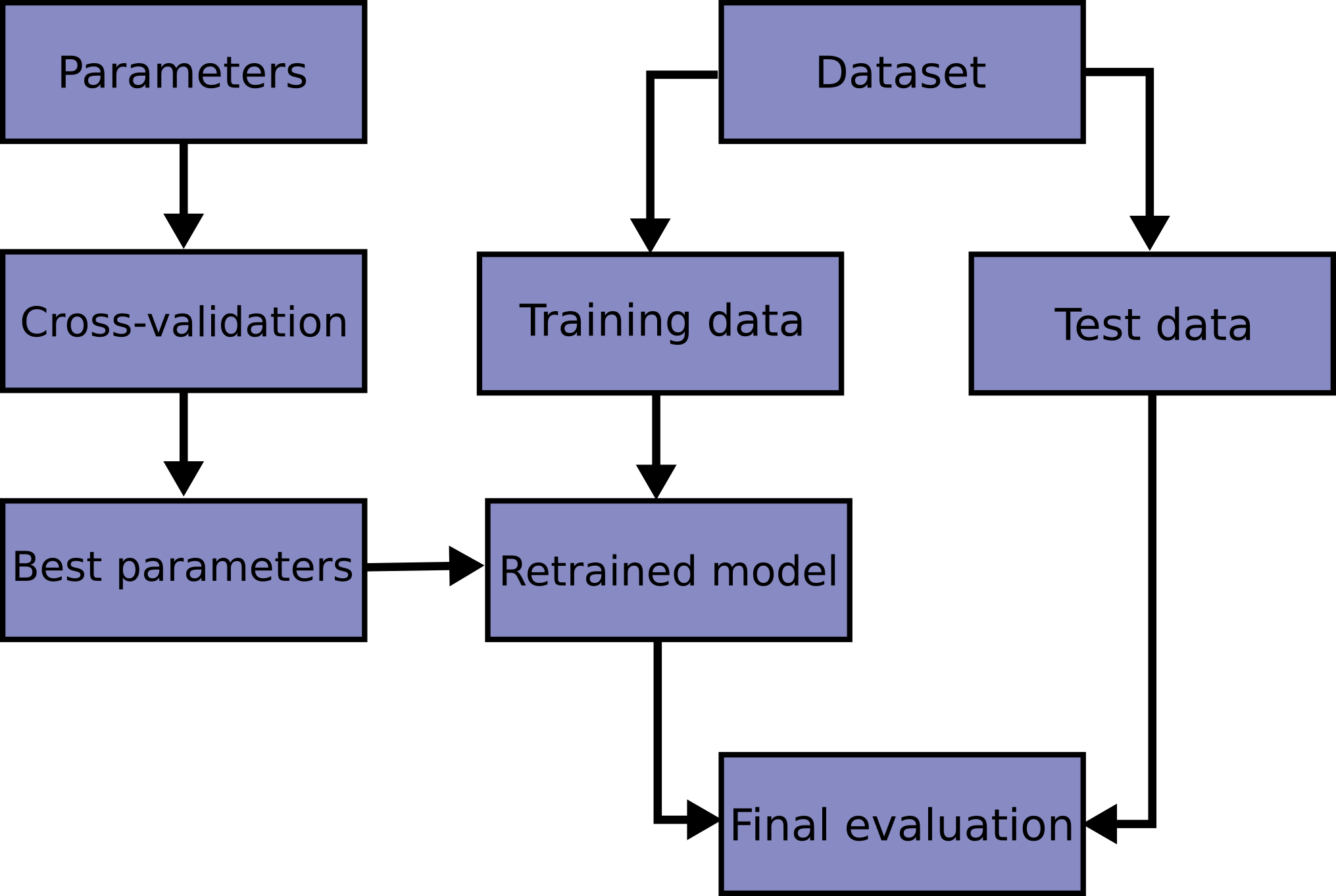
For example if I want to test to different ensemble of hyperparameters for my model I can:
The first method is a simple validation but 30% of the data won’t serve for statistically calibrates the data. The second one uses all the data for the training.
Here is an explaining scheme of cross validation:
Leave-p-out cross-validation involves using \(p\) observations as the validation set and the remaining observations as the training set. It is an exhaustive cross validation methods as it will try all possible combinations of \(p\) data for validation ie, if the total number of data is \(n\), it will test \(n \choose p\) different combination of validation data.
In pratice this method is not used.
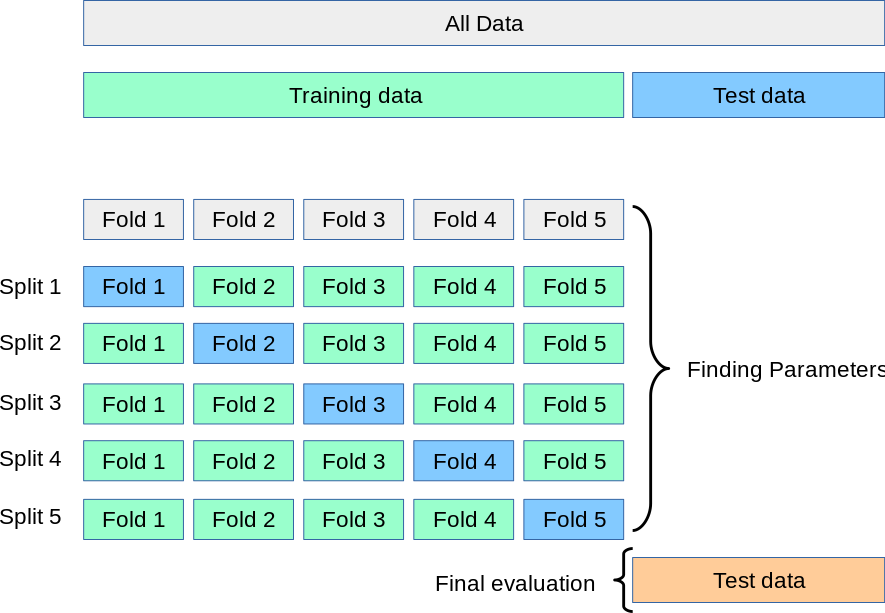
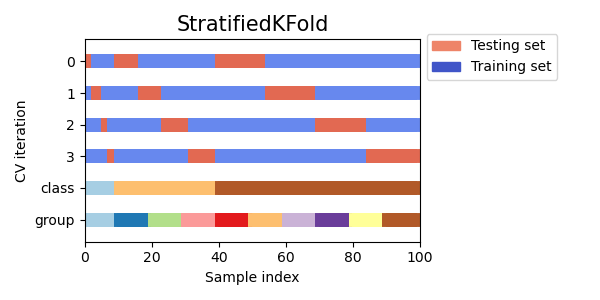
In k-fold cross-validation, the original sample is randomly partitioned into \(k\) equal sized subsamples. Of the \(k\) subsamples, a single subsample is retained as the validation data for testing the model, and the remaining \(k − 1\) subsamples are used as training data. The cross-validation process is then repeated \(k\) times, with each of the \(k\) subsamples used exactly once as the validation data. The \(k\) results can then be averaged to produce a single estimation.
The advantage of this method is that all observations are used for both training and validation, and each observation is used for validation exactly once.
10-fold cross-validation is commonly used, but in general \(k\) remains an unfixed parameter.
(copied from paragpraph on k-folds from Wikipedia page on Cross validation).
Here is a representation of \(k\)-folds:
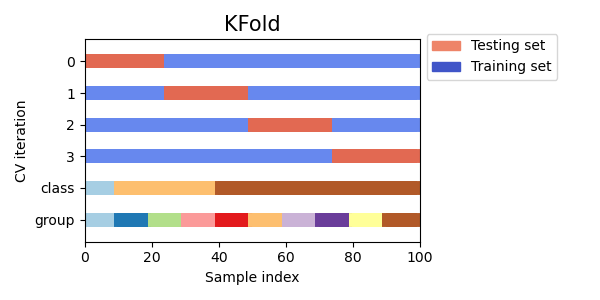
Here is another representation of \(k\)-folds:
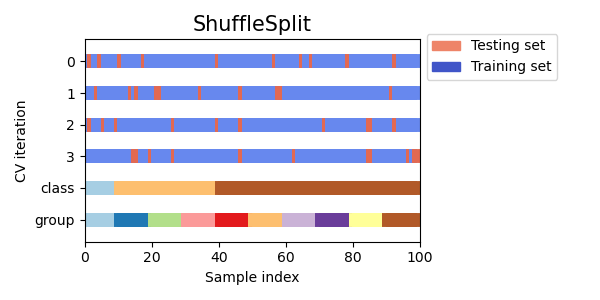
Suffle and Split method, also known as Repeated random sub-sampling validation (or Random permutations cross-validation or Monte Carlo cross-validation), generates multiple random splits of the dataset into training and validation data. The samples are first shuffled and then split into a pair of train and validation sets.
For each such split, the model is fit to the training data, and predictive accuracy is assessed using the validation data. The results are then averaged over the splits.
The advantage of this method (over \(k\)-fold cross validation) is that the proportion of the training/validation split is not dependent on the number of iterations (i.e., the number of partitions). The disadvantage of this method is that some observations may never be selected in the validation subsample, whereas others may be selected more than once. In other words, validation subsets may overlap. This method also exhibits Monte Carlo variation, meaning that the results will vary if the analysis is repeated with different random splits.
As the number of random splits approaches infinity, the result of repeated random sub-sampling validation tends towards that of leave-p-out cross-validation.
(copied from paragpraph on Repeated random sub-sampling from Wikipedia page on Cross validation.
Here is a representation of Suffle and Split:
StratifiedKFold is a variation of k-fold which returns stratified folds: each set contains approximately the same percentage of samples of each target class as the complete set.
Here is a representation of stratified \(k\)-folds:
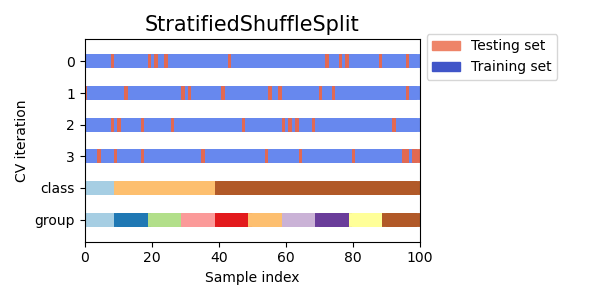
StratifiedShuffleSplit is a variation of ShuffleSplit, which returns stratified splits, i.e which creates splits by preserving the same percentage for each target class as in the complete set.
Here is another representation of stratified Suffle and Split:
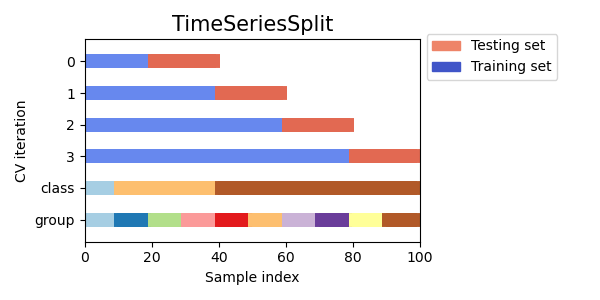
TimeSeriesSplit is a variation of k-fold which returns first \(k\)-folds as train set and the \((k+1)\)-th fold as test set. Note that unlike standard cross-validation methods, successive training sets are supersets of those that come before them. Also, it adds all surplus data to the first training partition, which is always used to train the model.
Older data are used more times than more recent data.
Here is a representation of Time Series split:
See: