
A Transformers model using attention block does not have any information about the positions or order of the words it uses.
However position and order of words are the essential parts of any language. They define the grammar and thus the actual semantics of a sentence. For example Recurrent Neural Networks (RNNs) inherently take the order of word into account; They parse a sentence word by word in a sequential manner. This will integrate the words’ order in the backbone of RNNs.
To counter this problem, positional encoding is used, which encodes the position of each word of a text.
The first idea that might come to mind is to assign a number to each time-step within the \([0, 1]\) range in which \(0\) means the first word and \(1\) is the last time-step. One of the problems of this method is that is can’t figure out how many words are present within a specific range. In other words, time-step delta doesn’t have consistent meaning across different sentences.
Another idea is to assign a number to each time-step linearly. That is, the first word is given \(1\), the second word is given \(2\), and so on. The problem with this approach is that not only the values could get quite large, but also our model can face sentences longer than the ones in training. In addition, our model may not see any sample with one specific length which would hurt generalization of our model.
The idea from Attention is all you need by A Vaswani and al. is to encode the position in \(d\) dimension (where \(d\) is the same dimension as the token encoding) using sinus and cosinus function:
\[PE_i(t) = \begin{cases} \sin(\omega_{i/2} \cdot t) \text{, if } i % 2 = 0\\ \cos(\omega_{(i/-1)2} \cdot t) \text{, if } i % 2 = 1\\ \end{cases}\]Where:
And where:
\[\omega_k = \frac{1}{10000^{2k/d}}\]With:
The frequencies are decreasing along the vector dimension. Thus it forms a geometric progression from \(2\pi\) to \(10000 \cdot 2\pi\) on the wavelengths.
Here is a visualisation of the \(d\)-dimensional vector \(PE\):

Here is a visual representation of a 128 dimensional sinusoidal positional encoding:
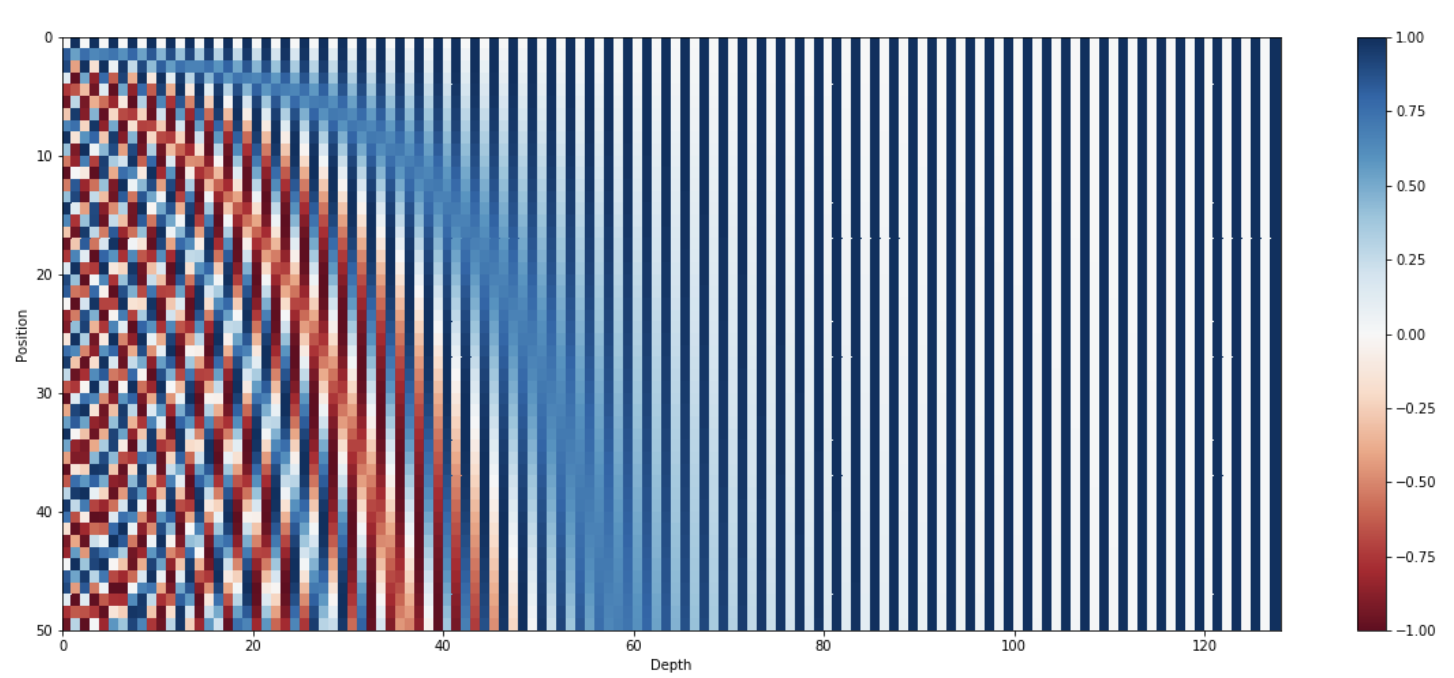
The token encoding and the positional encoding are just added. Recall that the two encoding are choosen to have the same dimension.
\[E(w_t) = PE(t) + WE(w_t)\]Where:
A intersting feature of sinusoidal positional encoding is that ‘it would allow the model to easily learn to attend by relative positions, since for any fixed offset \(k\), \(PE(t+k)\) can be represented as a linear function of \(PE(t)\)’.
It means that, for any offset \(k\), the relation between 2 tokens separated by \(k\) does not depend on the position of these two 2 tokens.
See:
See: