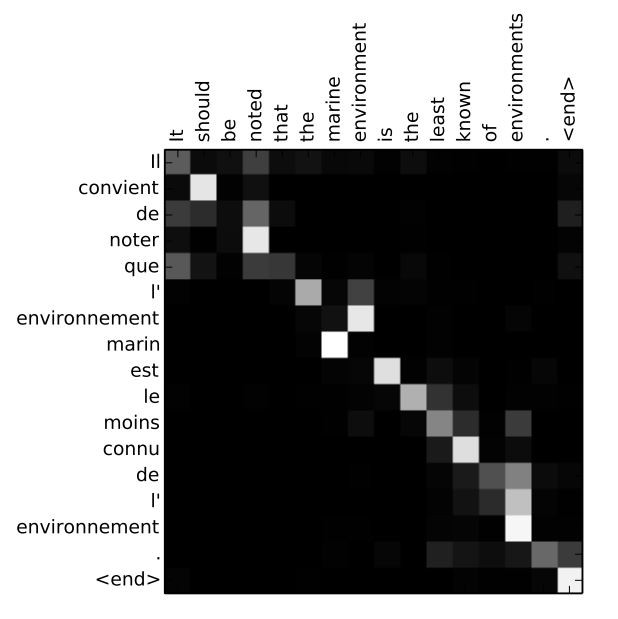
Attention is a block of transformers network that defines at each step of the prediction which part of the input the model should look at.
For example in this image we can see for each predicted word (in French) which input words (in English) have been used to predict this specific french word:

In a Transformer an attention block can be computed using different pairs of 3 values (Query, Keys and Values).
Here is an introductive example using the decoder hidden layer of the previous step (\(s_{i-1}\)) as Query and the encoder hidden layers (\(h_1, \ldots, h_n\)) as Keys and Values.
For a given decoder hidder layer \(s_{i-1}\), for every encoder hidden layer \(h_j\), the attention block computes a score
\[e_{i,j}=f(W^Q s_{i-1}, W^K h_j)\]Where:
It then uses these score to compute a softmax function (make the score sums to 1). This gives a weight \(\alpha_j\) for each hidden layer of the encoder:
\[\alpha_{i,j} = softmax(e_{i,j}) = \frac{e_{i,j}}{\sum_{l=1}^n e_{i,l}}\]\(\alpha_{i,j}\) represents the importance of hidden layer \(h_j\) for the current Query \(s_{i-1}\).
It then uses these weights \(\alpha_{i,j}\) to make a weighted average of the Values (\(h_1, \ldots, h_n\)) for the current Query \(s_{i-1}\):
\[c_i = \sum_{j=1}^k \alpha_{i,j} \left(W^V h_j\right)\]Where:
We saw that the attention block uses an alignement function \(f\) that we did not define.
A typical choice for \(f\) is the basic dot product will lead to the dot production attention:
\[f(Q,K) = Q^T K\]An attention block can be view as a query applied to keys to output some values with:
The query asks something to the keys (which hidden layers are the most relevant for this particular prediction?) that answered with the appropriate value.
\[\begin{eqnarray} \text{Attention}(Q,K,V) &&= softmax(Q^T K)V \\ &&= \frac{Q^T K}{\sum_{l=1}^k (Q^T K_l} V \;\;\; \forall j \in \{1, \ldots, n\} \end{eqnarray}\]Here \(f\) is a dot production function.
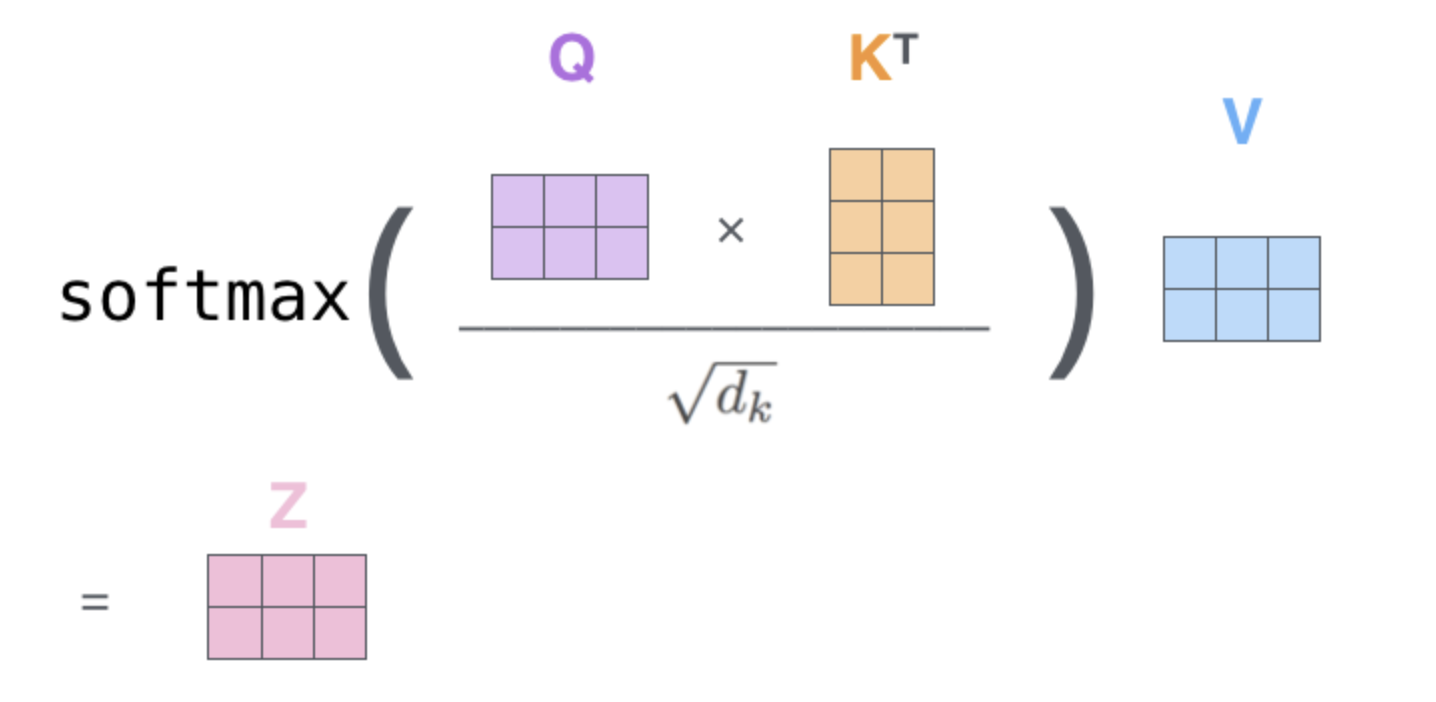
Here is a visualisation of an attention block in matrix form. From the illustrated Transformer by Jay Alammar.
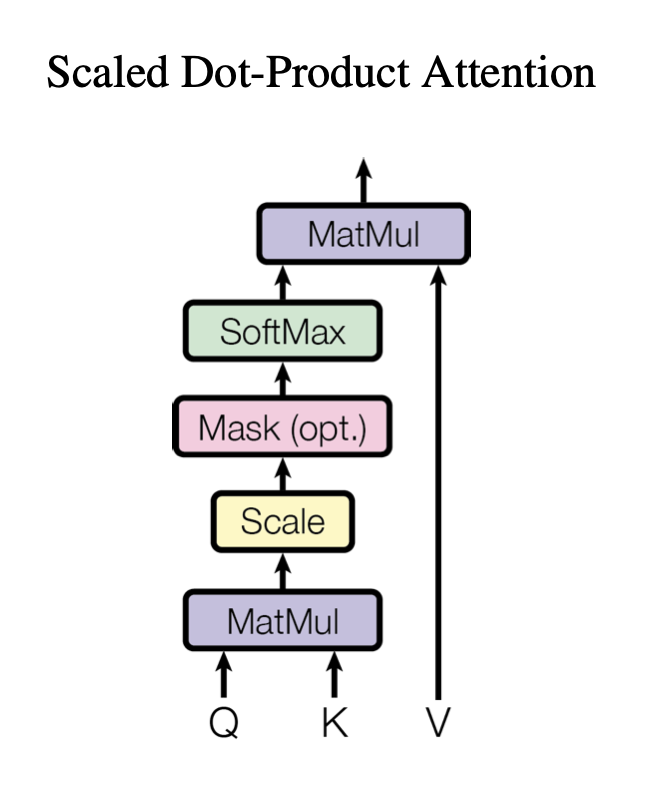
In the original paper they add a scaling factor \(\frac{1}{\sqrt{d_k}}\) in the softmax function where \(d_k\) is the dimension of the key vectors (64 in the original paper).
Here is a representation from the original paper of scaled dot product attention:
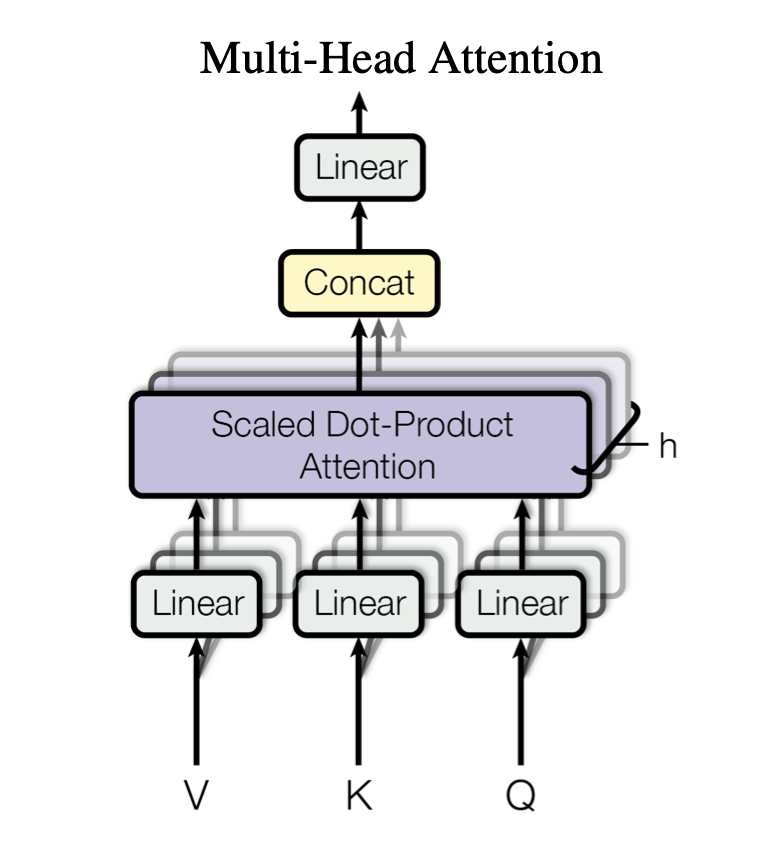
Multi-Head Attention is a generalisation of scaled dot product attention for \(Q\), \(K\) and \(V\) which project linearly \(Q\), \(K\) and \(V\) \(h\) times with learned weights (parameters) and then apply \(h\) scaled dot product attention on each of the projected pairs.
\[\begin{eqnarray} \text{Mulit-Head Attention}(Q,K,V) &&= \text{Concat}(head_1, \ldots, head_h)W^O \\ \text{Where } head_i &&= \text{Attention}(Q W_i^Q, K W_i^K, V W_i^V) \end{eqnarray}\]Where:
Here is an illustration of Multi-Head Attention:
From The illustrated Transformer by Jay Alammar:
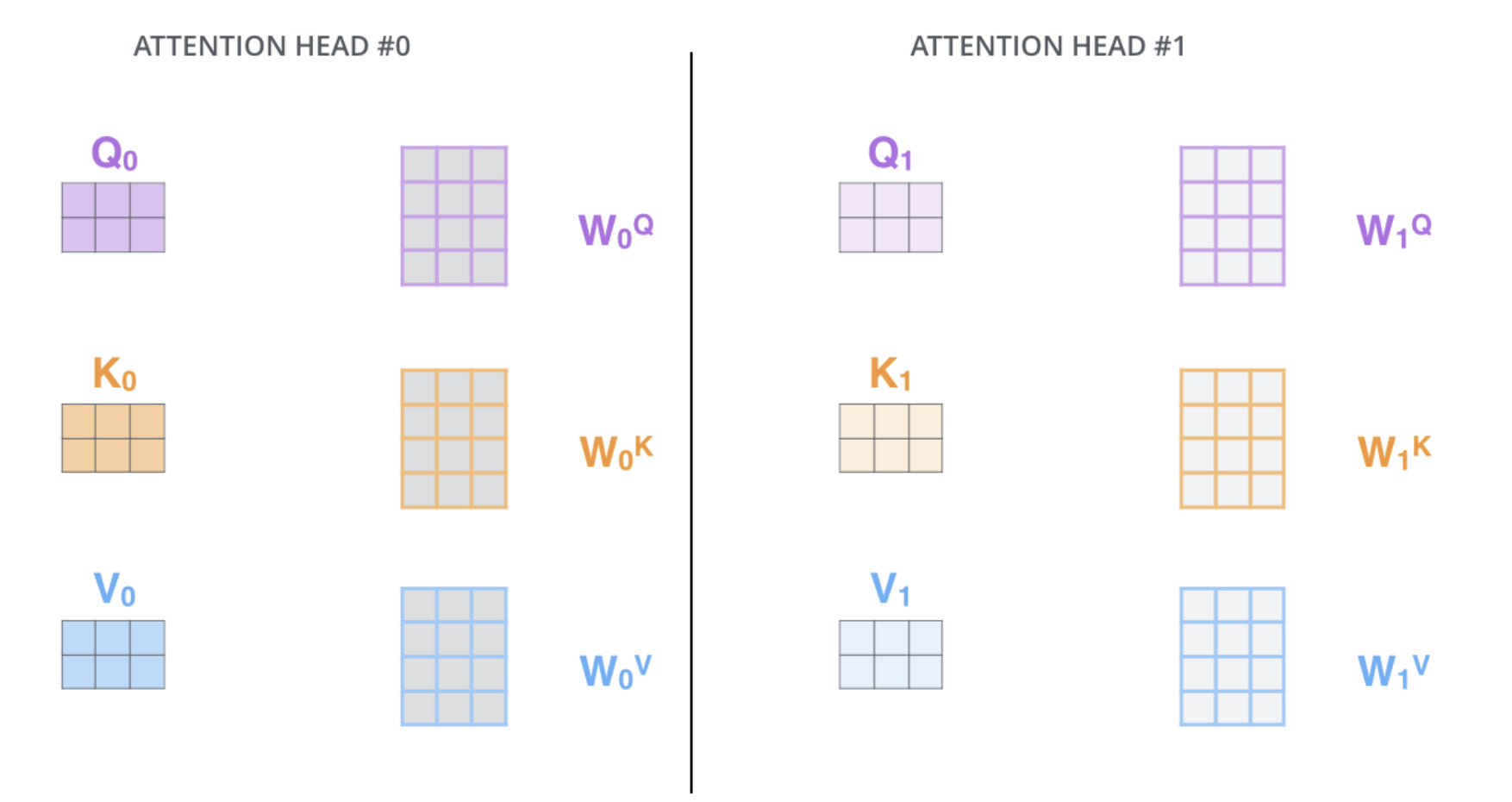
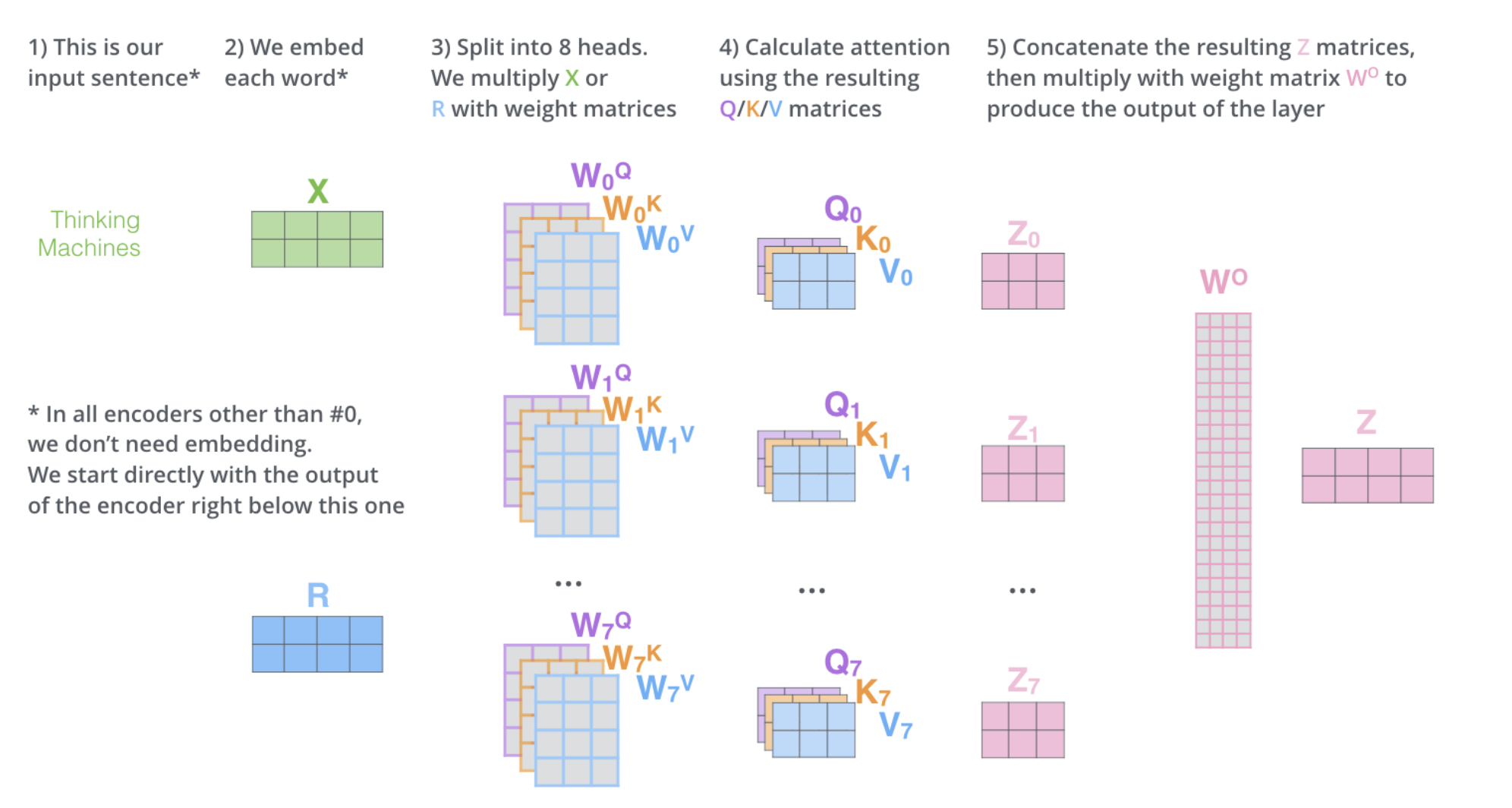
Here is a visualisation of 2 different heads of a multi-head attention block. Each head has its own projection matrix. This projection matrix are randomly initialized and are then updated during the training.
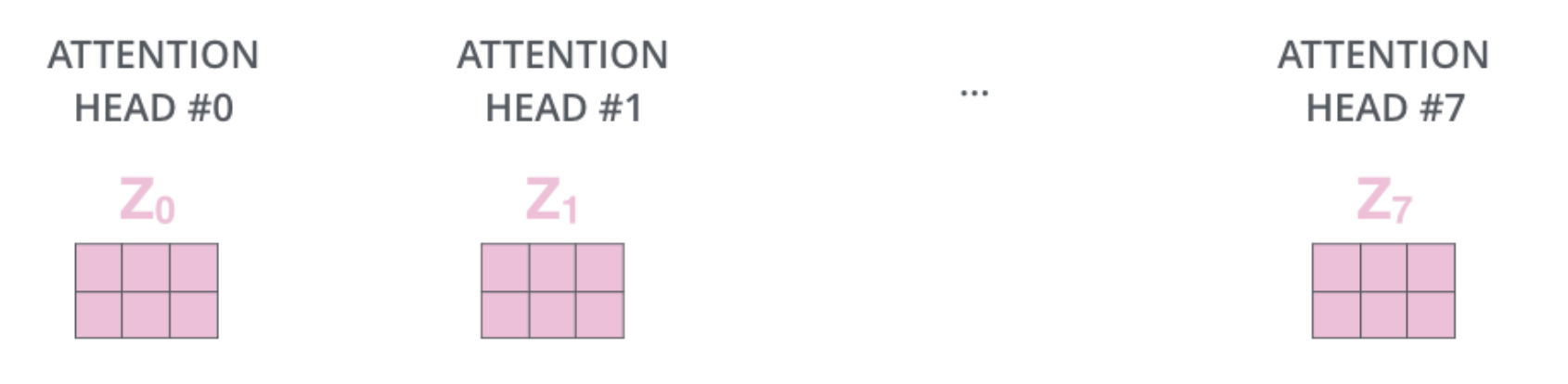
Here is a visualisation of the outputs of 8 heads of a multi-head attention block. 8 is the number of heads in the architecture of the Transformer from Attention is all you need by A Vaswani and al..
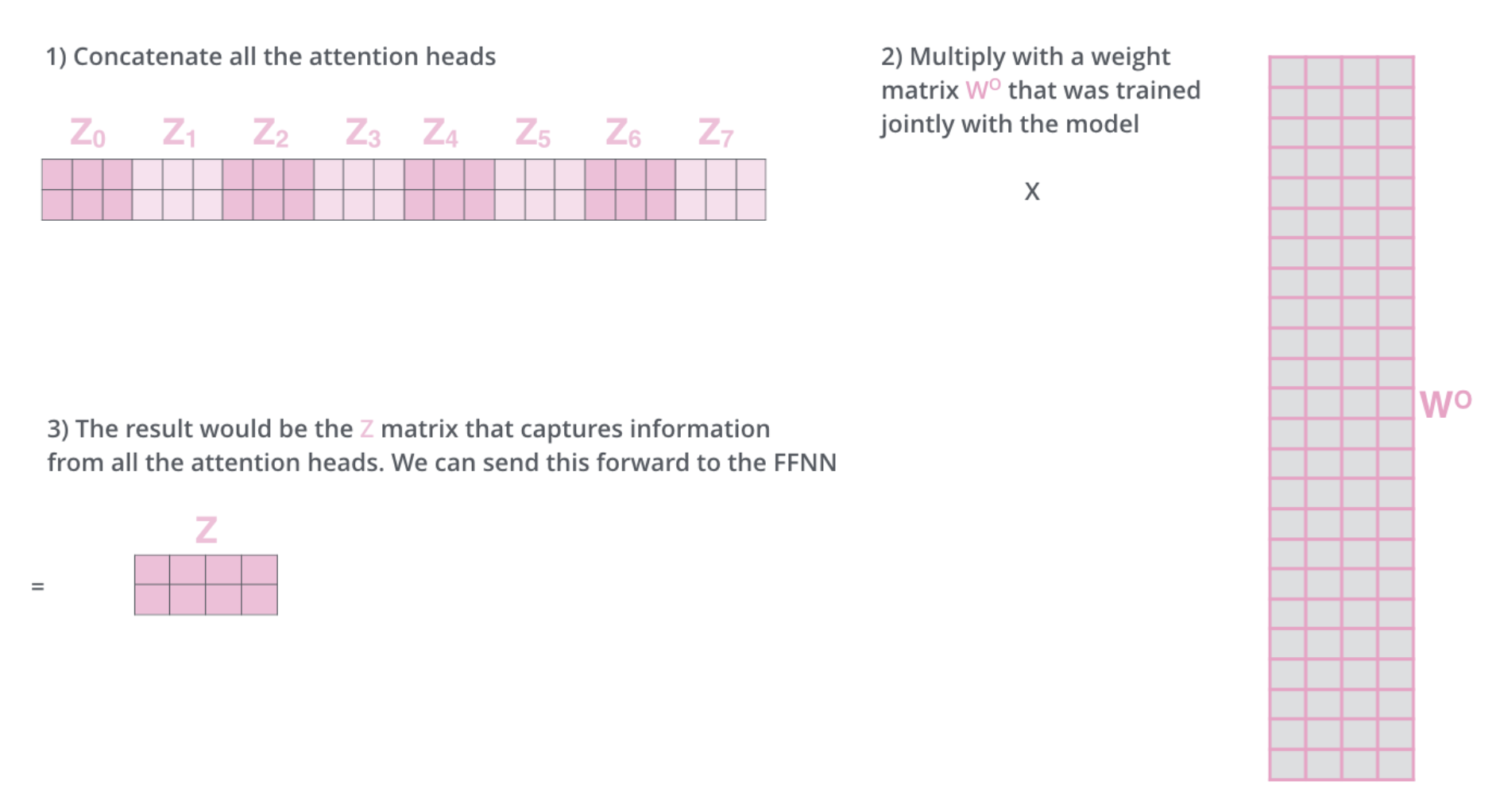
Here is a visualisation of the concatenation step which concates the 8 outputs of the 8 heads and then mutiply them by a projection matrix \(W^O\) to project the concatenation to a constant size vector (size \(d\), the same size as query, keys and values).
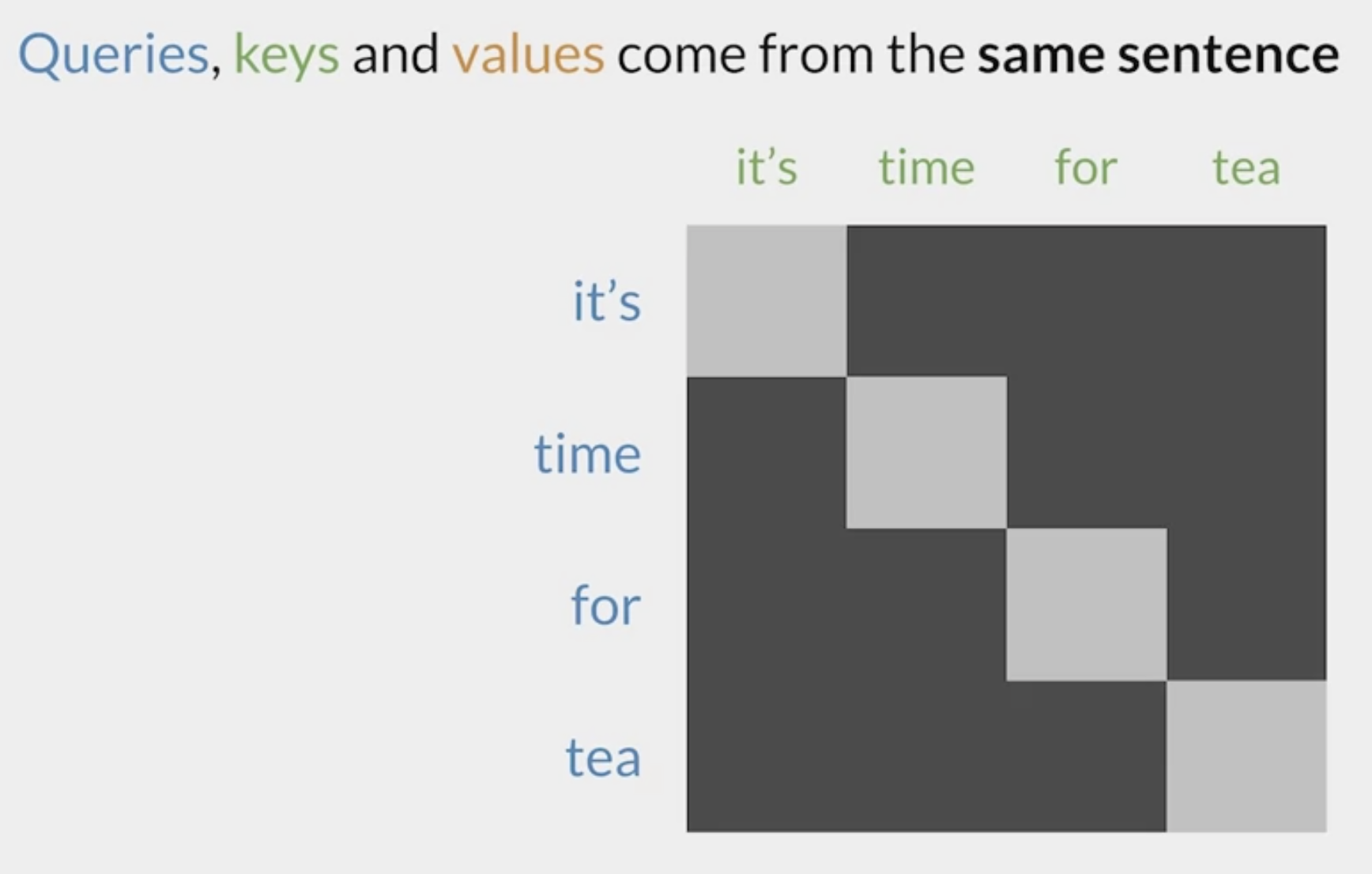
Self Attention is a special case of attention block which uses the same vectors (vectors from the layers coming as input of the self-attention block) for Query, Keys and Values:
The focus of a self attention layer is on itself:
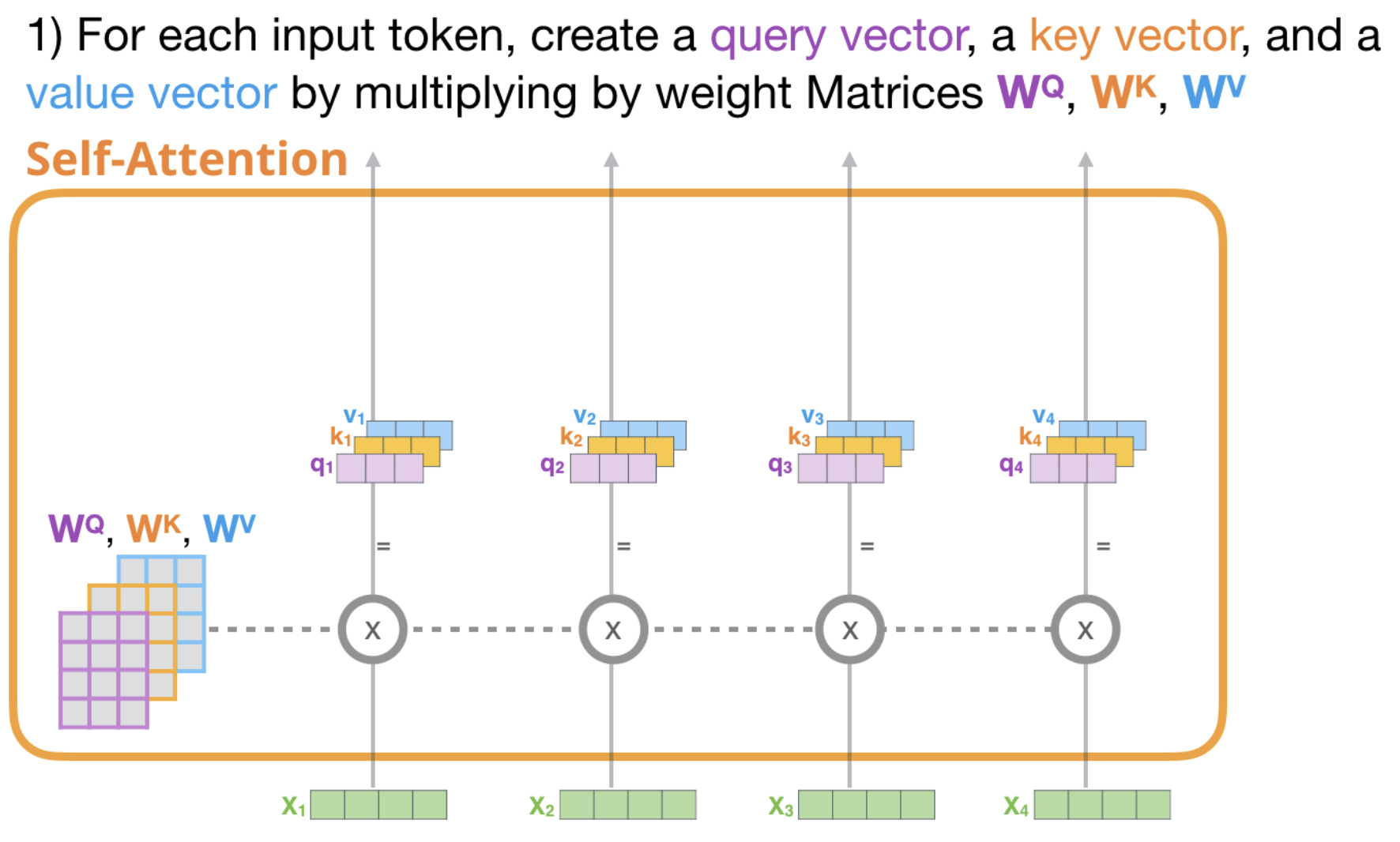
Here is an illustration of the projection of the vectors from the input layer (it could be an hidden layer) to Query, Keys and Values:
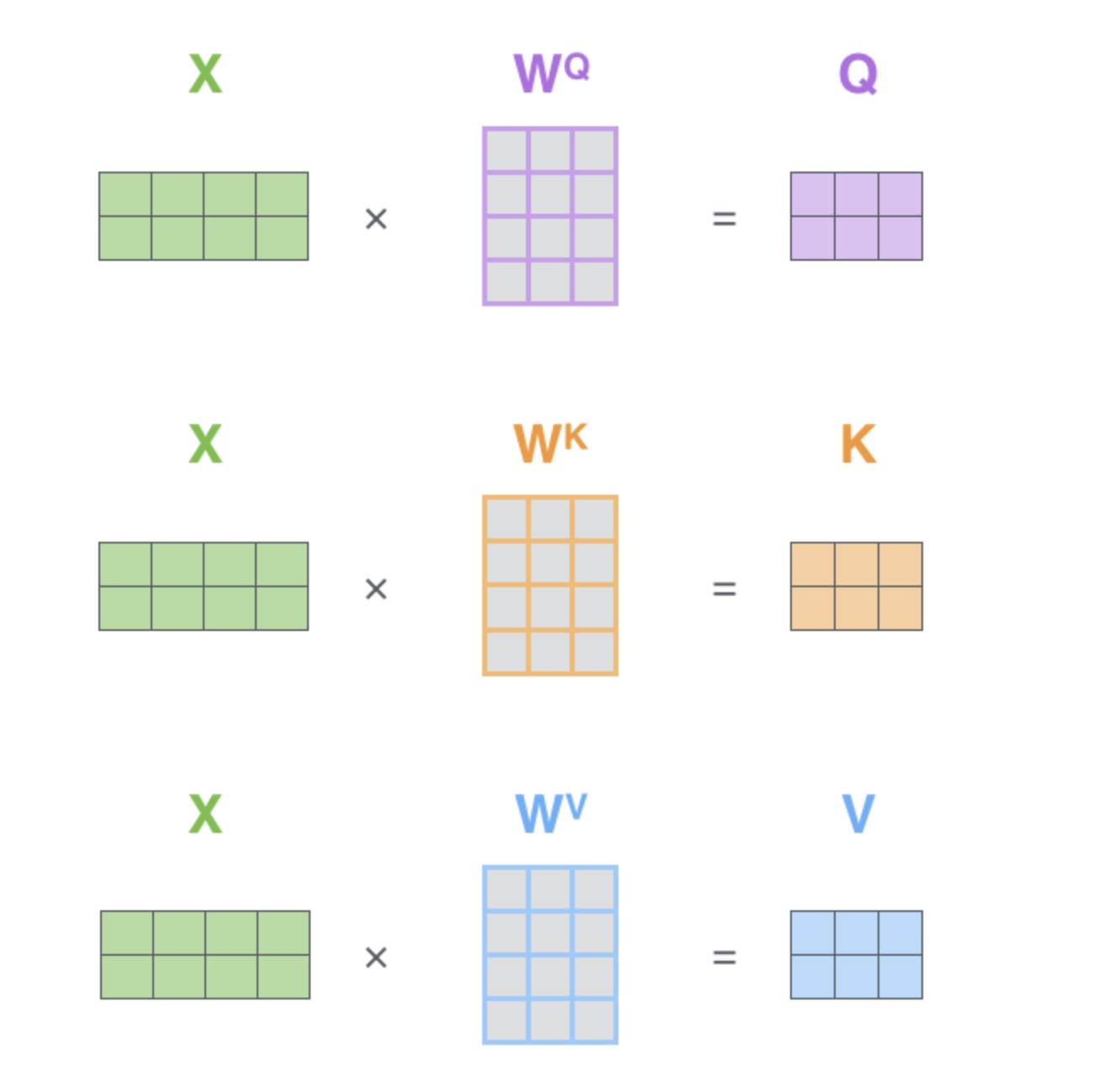
Here is an illustration of the self-attention block functionment for the first layer (input layer but it could be from any hidden layer) from the illustrated Transformer by Jay Alammar:
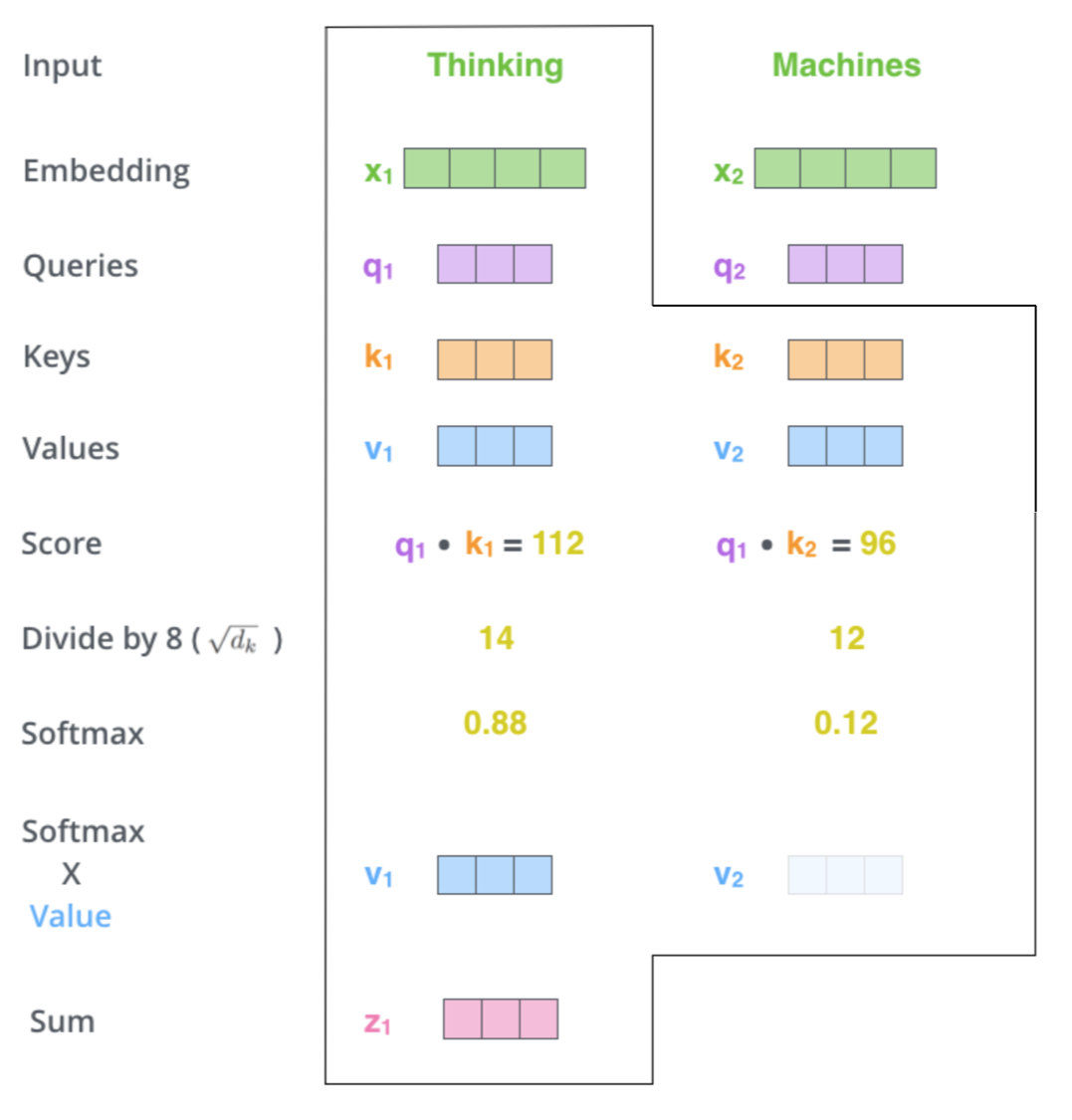
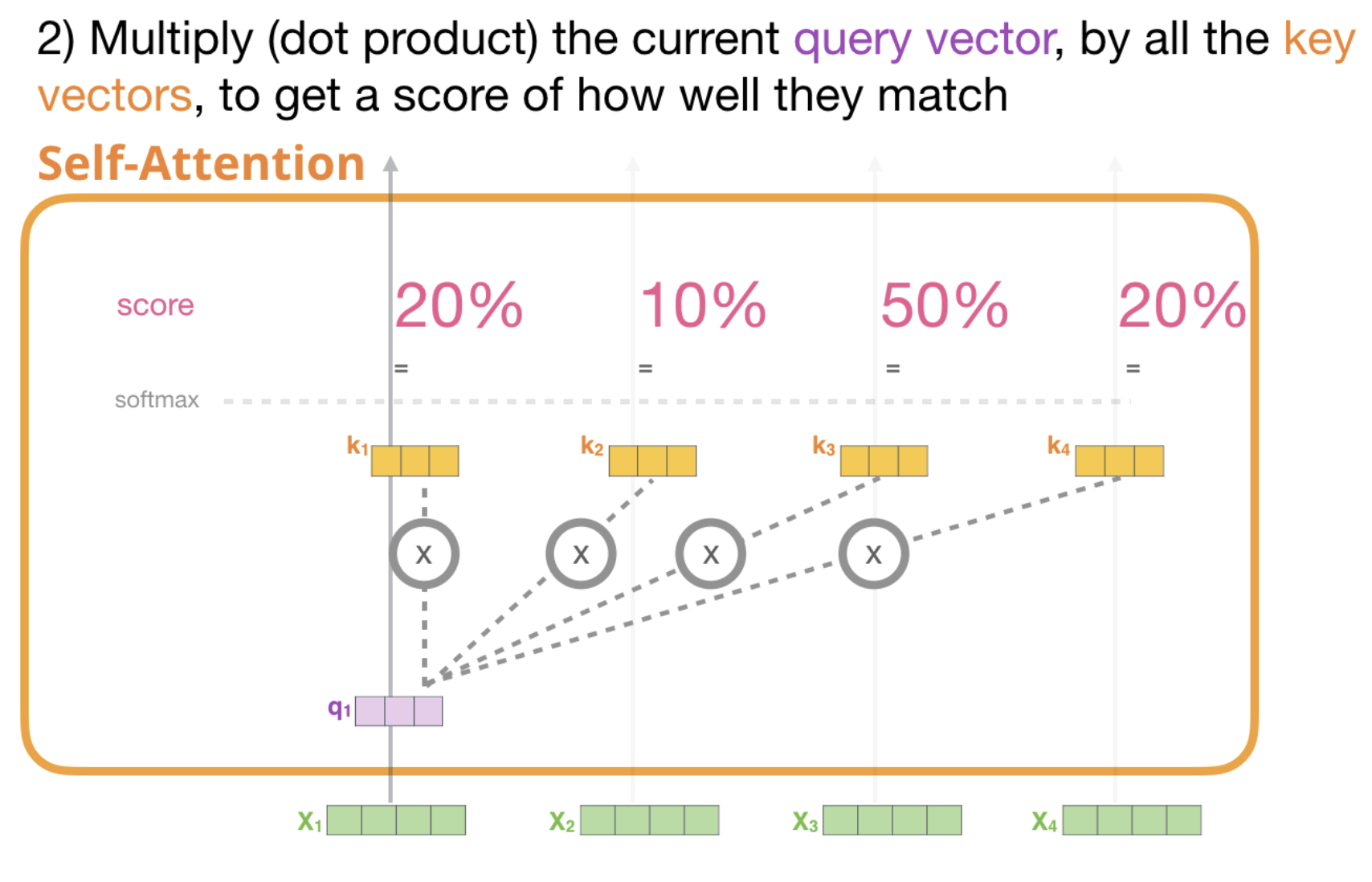
The block uses its projected Query vector and the projected Keys and Values vectors of every input. It then computes a score, rescales it, applies softmax and multiplies the Values vector by it.
The detail of the steps are exactly the same for a Single head attention block which would not be ‘self attention block’. The only difference would be that Query, Keys and Values vectors would not come from the same input.
Another more detailed illustration coming from The illustrated Self-Attention by Jay Alammar is as follow:
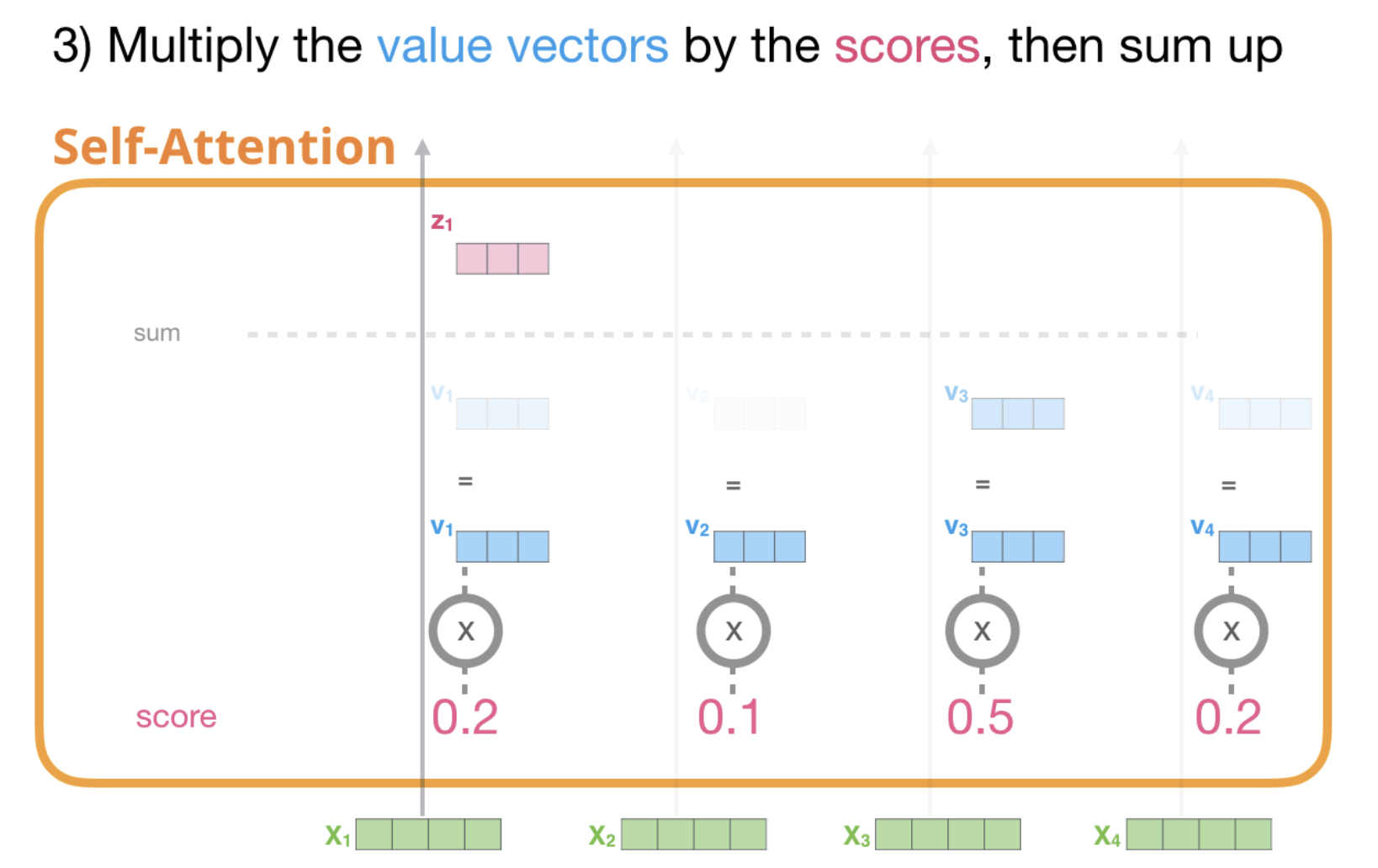
Finally we end up with a vector representing each token containing the appropriate context of that token. Those are then presented to the next sublayer in the transformer block:
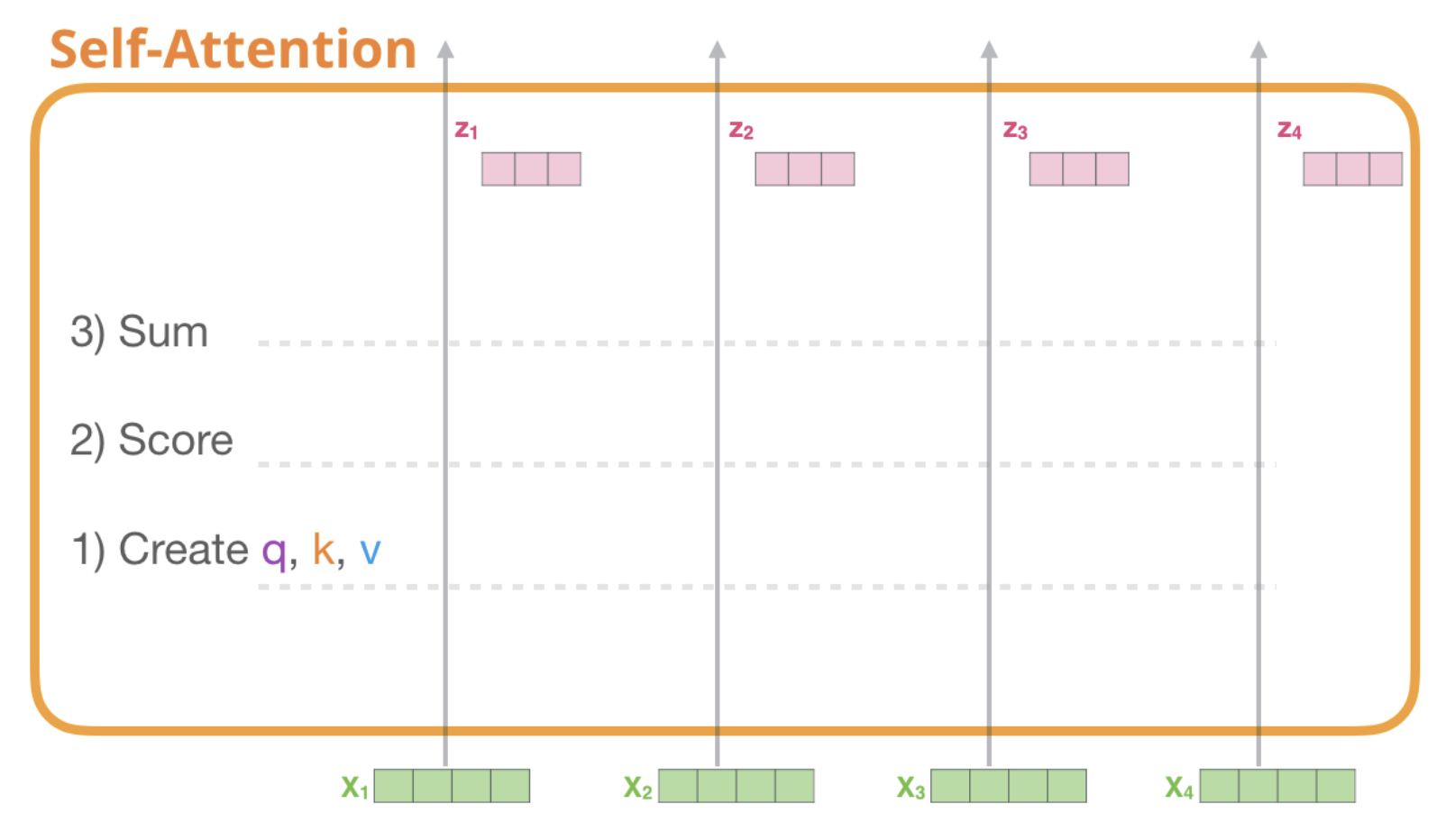
Here is a summary of a multi-head self attention block apply to the first layer (input layer) from the illustrated Transformer by Jay Alammar:
The detail of the steps are exactly the same for a Multi head attention block which would not be ‘self attention block’. The only difference would be that Query, Keys and Values vectors would not come from the same input.
A masked multi-head attention is simply a multi head attention in which some of the values are masked, ie they can’t be used by the attention block:
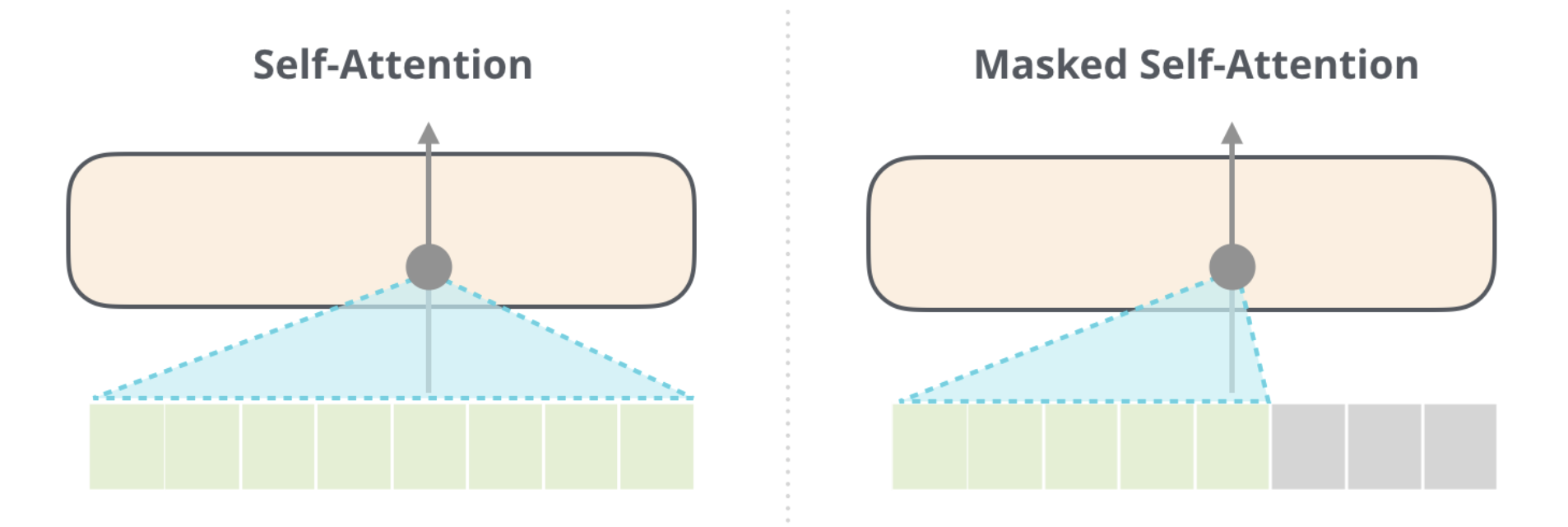
In the decoder part of a Transformer, the true output is used as an input. In a task like prediction of the next word, it is mandatory to mask the next words of the sentence otherwise the desired results would be in the input.
Here is a representation of masked attention: the model can only use information from previous words:

From a mathematical point of view, the mask is just an additional matrix that the block adds to the score \(e_{i,j}\) before computing the softmax:
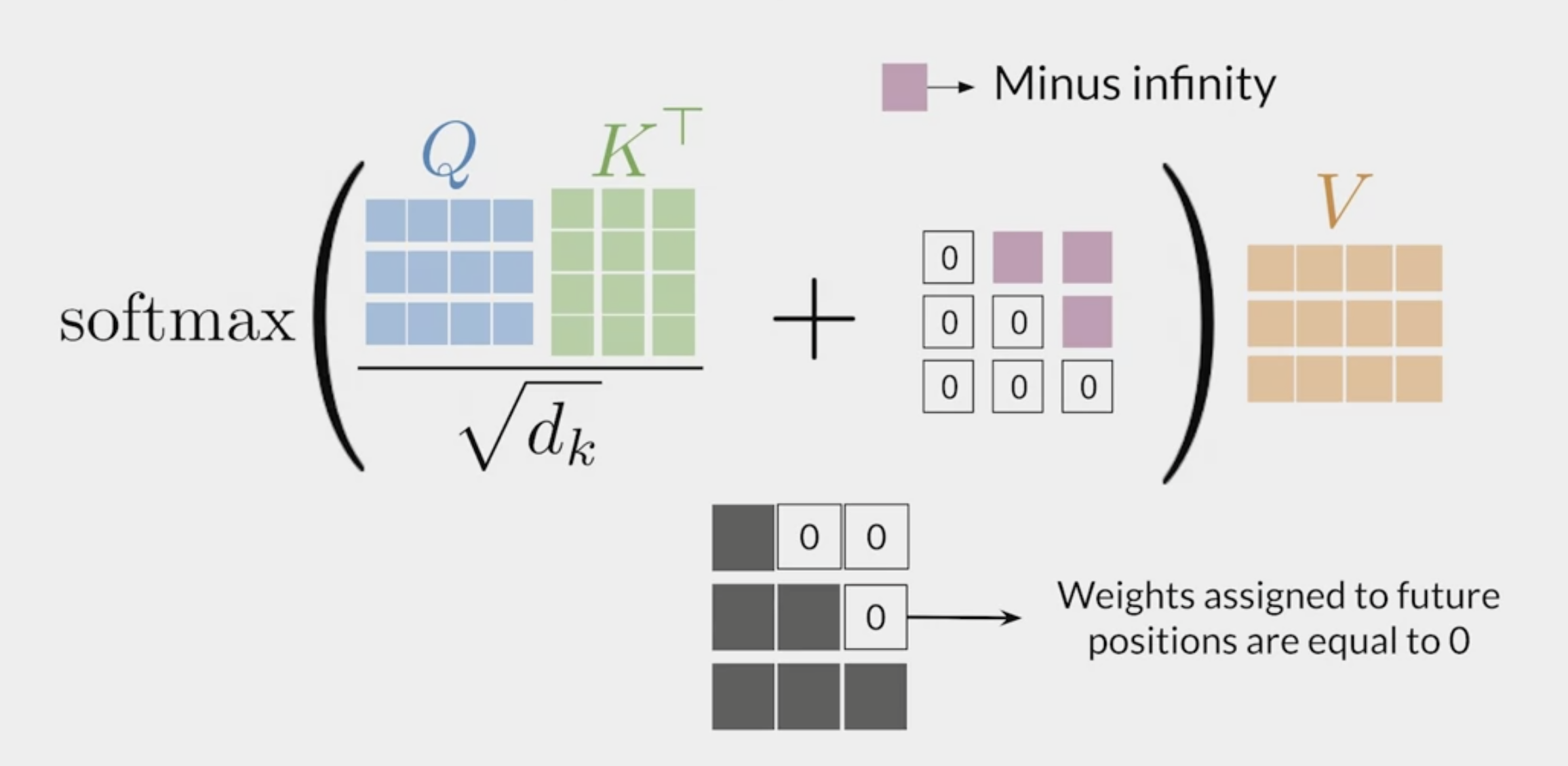
The addition of \(-\infty\) to every masked Values scores insure that these values won’t be used in this attention block.
Here is an illustration coming from The illustrated Self-Attention by Jay Alammar using a 4 words sentence in the task of next word prediction:

To predict true label ‘must’, the model can only look at the previous words ie ‘they’. To predict 3rd word ‘obey’, the model can look at previous words ie ‘they’ and ‘must’. The mask self attention block masks the other words.
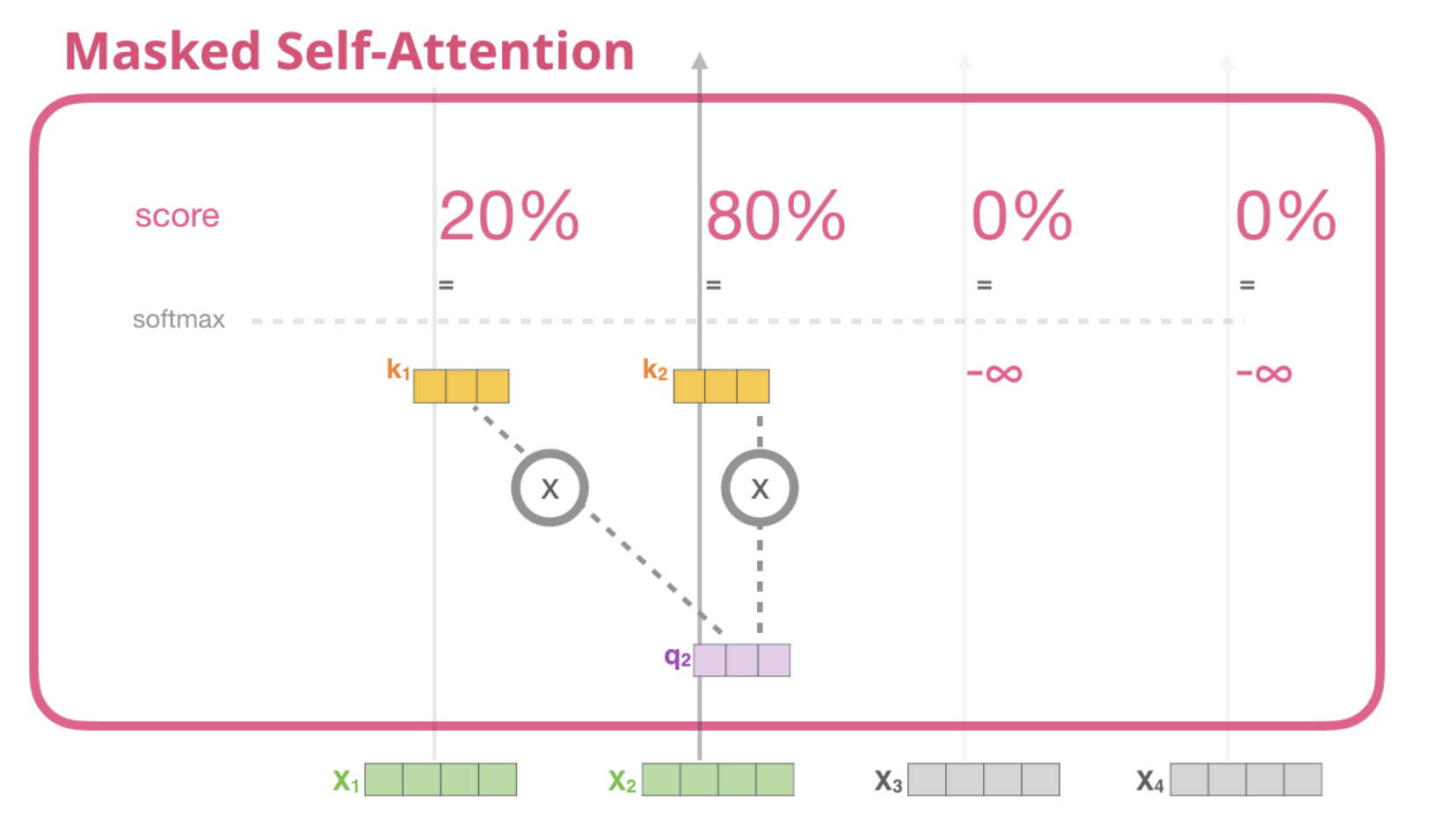
The input values after the current value are masked: their scores are set to \(-\infty\).
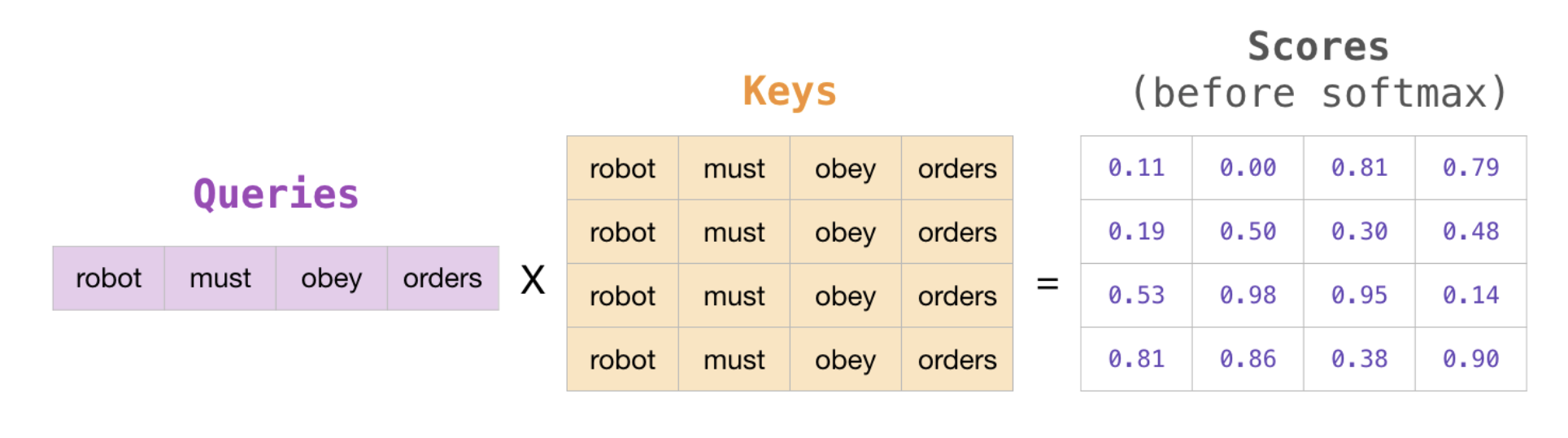
This first step of a mask attention block is classic and computes the scores for a Query (here it is done for multiple Queries at a time) and Keys.

Next the self-attention block just adds a matrix of \(0\) and \(-\infty\) to the score matrix. This mask matrix is upper diagonal with values \(-\infty\).

Using the softmax function, every Values associated to score which have been masked will be ignored (weight of 0).
Encoder-Decoder attention is an attention block for which, the Keys and Values come from the encoder and the Query comes from the Decoder. Encoder-Decoder attention is the second attention block of the decoder in the original Transformer from Attention is all you need by A Vaswani and al..

The “Encoder-Decoder Attention” layer works just like multiheaded self-attention, except it creates its Queries matrix from the layer below it, and takes the Keys and Values matrix from the output of the encoder stack.
See: