Reinforcement Learning is an area of machine learning concerned with how intelligent agents ought to take actions in an environment in order to maximize the notion of cumulative reward.
More formally the agent takes actions in the environment and these action lead him to win some rewards and lead him to new states with a new possible ensembles of actions.
Learning an agent to play a video game is an example of Reinforcement Learning. For example in Super Mario, a positive reward would be rewarded if the agent reach the end of the level and a negative reward would be given if the agent loose (fall in a hole, touche a turtle , etc.).
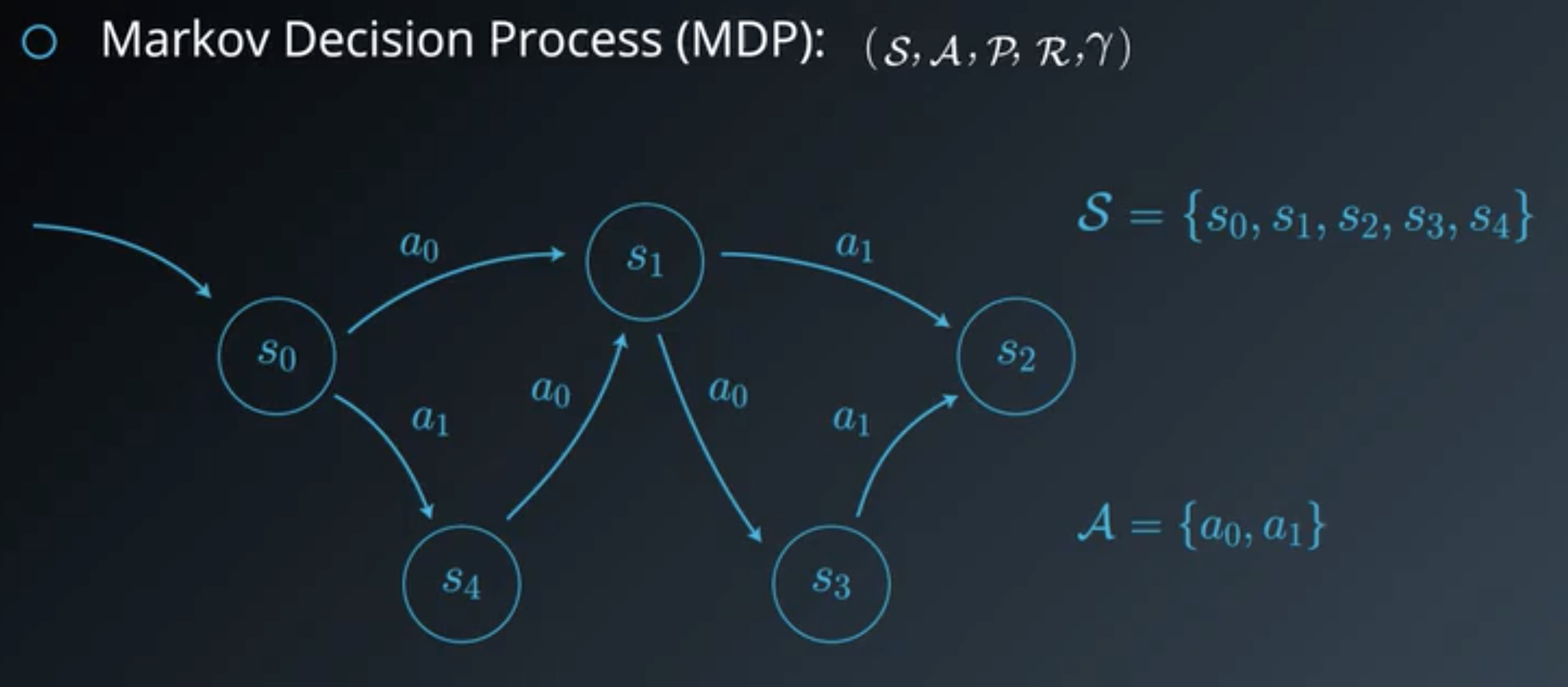
The environment is typically stated in the form of a Markov decision process.
A Markov Decision Process is defined by:

At each time we have a state, action and reward:
From the future reward and \(\gamma\), we can define:
The states \(\mathcal{S}\) and the possible actions \(\mathcal{A}\) are genrally known by the agent but not the rewards \(\mathcal{R}\) neither the dynamic \(p(s',r \; \vert \; s,a)\) of the environment.
The agent will follow some strategies (policies) to deal with the environment.
In a deterministic environment, the policy for an agent is an action for each state.
In a stochastic environment it is a probability distribution of actions for each state.
A deterministic policy associates a single action \(a\) to a state \(s\). That means that in state \(s\) the same action \(a\) will always be choosen.
A stochastic policy, on the other hand, associate to each state \(s\) a probability for every possible action \(a\).
The state-value function \(v_{\pi}\) for a given policy \(\pi\) returns an extpected value of rewards for each state \(s\):
\[v_{\pi}(s) = \mathbb{E} [G_t \vert S_t=s] \forall s \in \mathcal{S}\]The optimal state-value function \(v_{*}\) is the state-value function associated with the policy \(\pi\) that maximises the reward for each state \(s\):
\[v_{*}(s) = \max_{\pi} v_{\pi}(s) \forall s \in \mathcal{S}\]The action-value function \(q_{\pi}\) for a given policy \(\pi\) returns an extpected value of rewards for each state \(s\) and each \(action\):
\[q_{\pi}(s,a) = \mathbb{E} [G_t \vert S_t=s, A_t=a] \forall s \in \mathcal{S} \text{ and } \forall a \in \mathcal{A}(s)\]The optimal action-value function \(q_{*}\) is the action-value function associated with the policy \(\pi\) that maximises the reward for each state \(s\) and action \(a\):
\[q_{*}(s, a) = \max_{\pi} q_{\pi}(s, a) \forall s \in \mathcal{S} \text{ and } \forall a \in \mathcal{A}(s)\]
See:
Bellman equations are a set of dynamic programing equation that expresses the state-value and action-value functions of a state \(s\) (and action \(a\)) using next states and actions.
The state-value function \(v_{\pi}\) for a state \(s\) can be expressed as:
\[v_{\pi}(s) = \sum_{a \in \mathcal{A}(s)} \pi (a \vert s) \sum_{s' \in \mathcal{S}, r \in \mathcal{R}}p(s',r \; \vert \; s,a)(r + \gamma v_{\pi}(s'))\]
The Bellman optimal equation for value function is:
\[v_{*}(s) = \max_{a \in \mathcal{A}(s)} \sum_{s' \in \mathcal{S}, r \in \mathcal{R}}p(s',r \; \vert \; s,a)(r + \gamma v_{*}(s'))\]The optimal state-value function \(v_{*}\) is defined as an application of its definition: it is the reward associated with the action that maximises this reward.
The action-value function \(q_{\pi}\) for a state \(s\) and action \(a\) can be expressed as:
\[q_{\pi}(s,a) = \sum_{s' \in \mathcal{S}, r \in \mathcal{R}}p(s',r \; \vert \; s,a) \left(r + \gamma \sum_{a' \in \mathcal{A}(s')} \pi (a' \vert s') q_{\pi}(s',a') \right)\]The Bellman optimal equation for action function is:
\[q_{\pi}(s,a) = \sum_{s' \in \mathcal{S}, r \in \mathcal{R}}p(s',r \; \vert \; s,a) \left(r + \gamma \max_{a' \in \mathcal{A}(s')}\right)\]See: