
Dynamic programming (DP) is used for finite environment. DP is a model based learning method based on dynamic programming and the Bellman’s equations.
In this setup (environment with finite number of states and actions where the model is known ie with known rewards \(r\) and transitions probabilities \(p(s',r \; \vert \; s,a)\)) a simple application of Bellman’s equation is sufficient to estimate the state and action value functions.
This setup doesn’t require to leverage interactions between the agent and the environment.
The policy evaluation algorithm is used to estimate the value function associated with the policy.

One can set a maximum of iteration to avoid the algorithm to never stop.
Once the state value function has been estimated using the policy evaluation algorithm, one can easily estimate the action value function as follow:

Given a policy \(\pi\) and its state value function \(v_\pi\), one can apply a policy improvement algorithm to obtain a new policy \(\pi'\) such that \(\pi' \geq \pi\) (ie \(v_{\pi'}(s) \geq v_{\pi}(s) \forall s \in \mathcal{S}\)):

For each state, the algorithm will estimate the best action to take using its state value function (or directly using its action value function). It will update the policy by associating the action \(a\) that maximises reward to the state \(s\).
The precedent policy \(\pi\), used to evaluate the state value function, used an equally weight probability for all action of a state in order to estimate the state value function (see Policy evaluation).
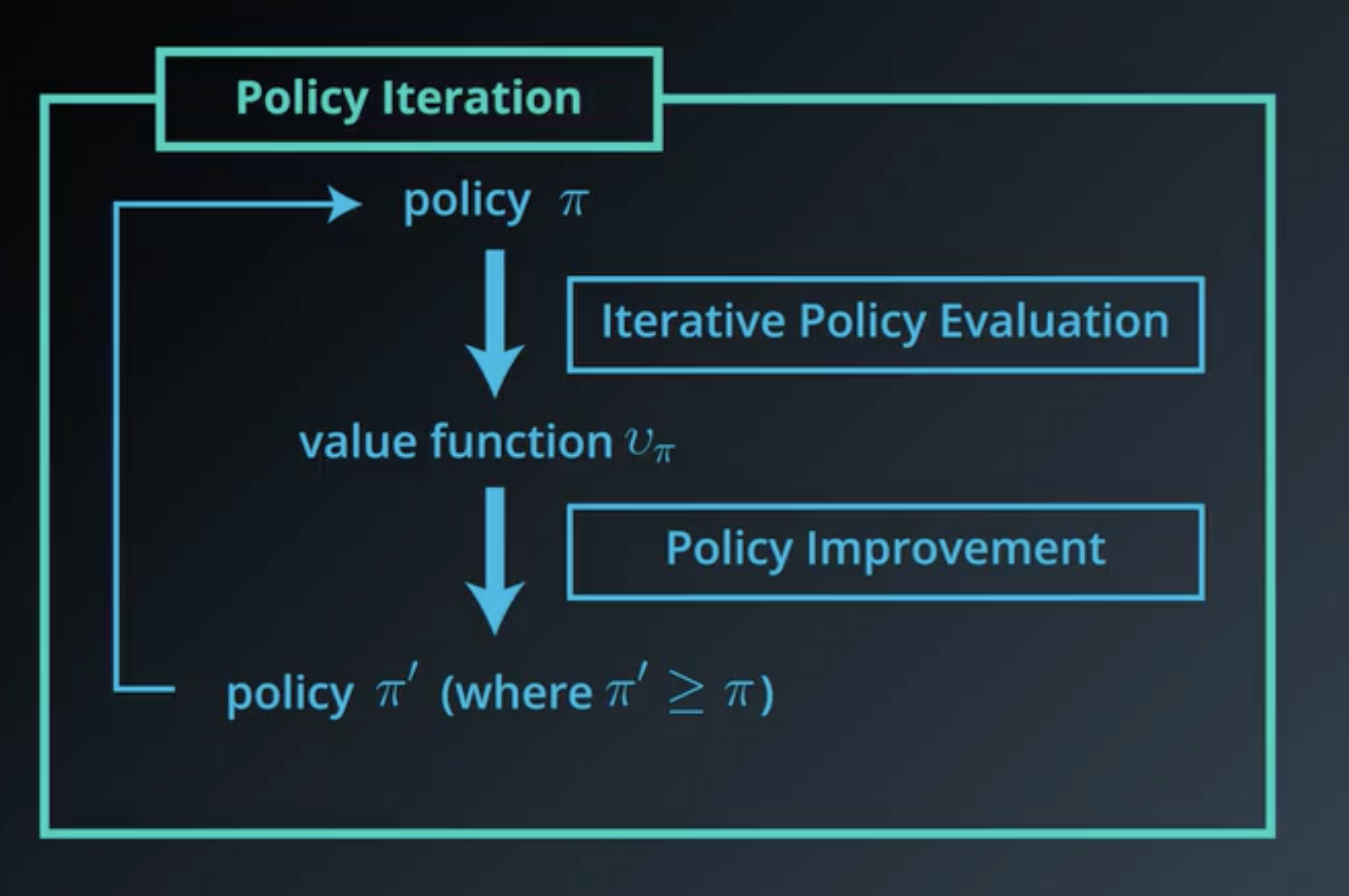
Using successively policy estimation and policy improvement, one can start with a simple (equiprobable) policy and improve it step by step:

The algorithm alternates between the two methods: ‘Policy evaluation’ and ‘Policy improvement’.
Here is a schematic view of the algorithm:
See: