
Actor-Critic method combines a policy based method ie an actor with a value based method ie a critic.

A policy based method directly estimates the policy. The neural network of the method directly outputs an action. Hence the model acts.
In the REINFORCE model, the Monte-Carlo method is used that wait until the end of a batch of episode before updating the model.
A value based method directly estimates the action value function. The model tries to guess what will be the associated reward for each action. The model does’nt act hence it can be viewed as a critic.
In the DQN model, the Temporal difference is used to estimate the action value function.
The actor critic method will use an actor and a critic:
The Monte-Carlo method used to train the actor will be modfied using the critic: the actor won’t need to wait a full episode to obtain an estimate of the return and to update its parameters using gradient ascent. It will now be able to apply temporal differences.
Here is a video that present the algorithm (click on the gif to download the video with oral explanations):
In the video, the actor is \(\pi\) with parameters \(\theta_\pi\) and the critic is \(V\) with parameters \(\theta_V\). First the actor takes an action and from the environment the model observes the reward and the next state. The critic uses this reward and next state to define its alternative estimate and update its parameters using TD estimate. Then the critic computes an estimate of total return \(G\) by computing the advantage value \(A(s,a)\) (see note on advantage value function) and adding it to the state value. The actor then uses this estimate of return to update its parameters.
The critic (with parameters \(\theta_V\)) computes an estimation of the total return \(G\) using the state value function of next state \(s'\) and reward \(r\).
The estimation of \(G_{\theta_V}\) from the critic is:
\[G = r + \gamma V_{\theta_V}(s')\]Where:
Once this estimation of the return \(G\) is obtained, the actor will use this information to update its parameter in order to better represent the reality of the environment.
More specifically it can be understood using the advantage function. Recall that the advantage function \(A(s,a)\) is the advantage of an action \(a\) with respect to a state \(s\). It is the difference between the action value function \(Q(s,a)\) and the state value function \(V(s)\):
\[A(s,a) = Q(s,a) - V(s)\]Also \(G_{\theta_V}\) is exactly the estimation of the reward obtained by taking action \(a\) in state \(s\). It is thus equivalent to the action value function \(Q_{\theta_V}(a, s)\).
Finally we can express the difference between the current estimate of the state function and the alternative estimate of the state function as:
So the actor will look at the advantage function of the action \(a\) it choosed. 2 possibles option arise:
Also note that the critic can compute the advantage function just by computing the state value function.
And here is the pseudo code of the algorithm:

The actor is \(\pi\) with parameters \(\theta\) and the critic is \(\hat{v}\) with parameters \(w\). The update rule for the critic is the same as the update rule of DQN. The update rule for the actor is the same as the update rule of REINFORCE.
Here is the detail of the gradient ascent update rule of the actor where we see the influence of the critic:
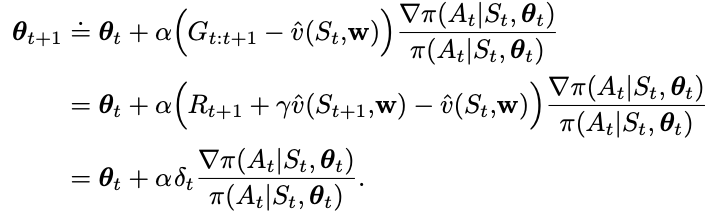
See: