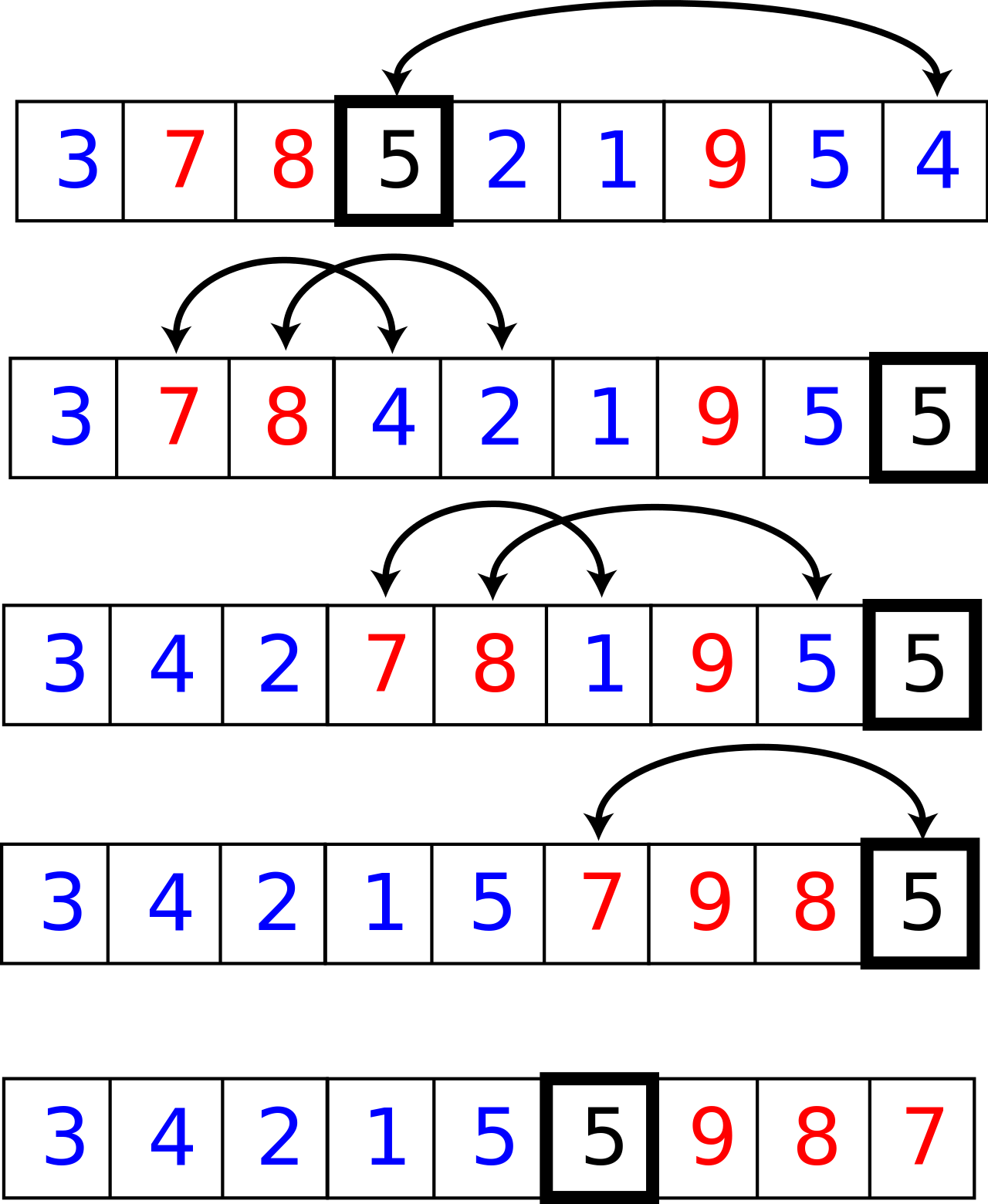
Visualisation from Wikipedia of the QuickSelect algorithm¶

def quickselect(left, right, nums):
# Last element will be the pivot and the first element the initial delimiter
pivot, delimiter = nums[right], left
for i in range(left, right):
if nums[i] <= pivot:
# Swapping values smaller than the pivot to the front
nums[i], nums[delimiter] = nums[delimiter], nums[i] # 'nums[i]' is now at the index 'delimiter'
delimiter += 1 # 'nums[i]' is now on the left of the delimiter
# Finally swapping the last element with the pointer indexed number
nums[delimiter], nums[right] = nums[right], nums[delimiter]
return delimiter
def quicksort_helper(left, right, nums):
# Call the algorithm if left < right ie there are elements to sort; otherwise the elements are already sorted
if left < right:
pivot = quickselect(left, right, nums)
quicksort_helper(left, pivot-1, nums) # Recursively sorting the left values
quicksort_helper(pivot+1, right, nums) # Recursively sorting the right values
return nums
def quicksort(nums):
return quicksort_helper(0, len(nums)-1, nums)
quicksort([2, 5, 6, 1, 4, 6, 2, 4, 7, 8])
[1, 2, 2, 4, 4, 5, 6, 6, 7, 8]