Definition
A Total Return Swap is a financial derivative contract between 2 party where the 2 party agree to exchange, at periodic dates, 2 cash flows. The buyer of the TRS agrees to receive the total performance of an asset or a basket of asset in exchange of paying a reference rate. Note that if the performance of the underlying is negative, the buyer is obliged to pay the value.
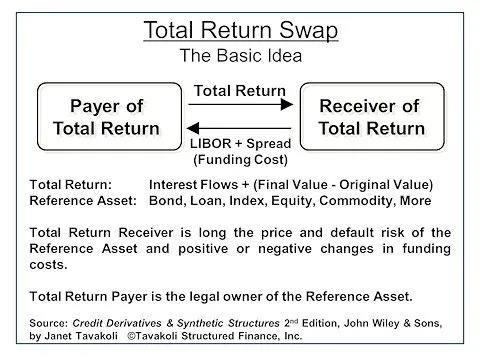
Here is a visual representation of flow exchanged in a TRS:
It is important to note that TRS are funding cost arbitrages products.
Advantages
- TRS allow an investor to enjoy all of the cash flow benefits of a security without actually owning the security,
- TRS are off balanced sheet asset (the asset owner retains ownership of the asset): an institutional investor who has surpassed its balance sheet capacity may still speculate (or hedge) through a TRS,
- TRS are leveraged derivatives: hedge fund can use TRS to take leveraged positions,
- Investors can create new assets with a specific maturity not currently available in the market,
- Investors can reduce administrative costs via an off balance sheet purchase,
- A long-term investor who feels that a reference asset in portfolio may widen in spread in the short term, but then will recover, may enter into a TRS which is shorter than the maturity of the asset.
\[\begin{cases}
\text{Leg}_{\text{Total Return}} && = N * \left(\sum_{i=1}^{T}\left[(B_{t_i} - B_{t_{i-1}}) + C_{(t_{i-1}, t_i)}\right] * DF_{t_i}\right)\\
\text{Leg}_{\text{Floating}} && = N * \left(\sum_{i=1}^{T} B_{t_{i-1}} * \left(DF_{t_i}^{financing}\right)^{-1} * DF_{t_i}\right)
\end{cases}\]
With:
- \(N\) being the notional of the TRS,
- \(B_{t_0}\) being the spot price of the underlying bond,
- \(B_{t_i}\) being the futur price of the underlying bond as seen at \(t_0\),
- \(C_{(t_{i-1}, t_i)}\) being the coupon received during the period between \(t_{i-1}\) and \(t_i\),
- \(DF_{t_i}\) being the risk free Discount Factor at time \(t_i\),
- \(DF_{(t_i)}^{financing}\) being the discount factor associated with the financing rate at time \(t_i\).
The repo rate is the key driver of the financing rate: if the holder of the collateral bond receive income from lending the bond at the repo rate, TRS would expect the spread to be subtracted from the financing cost.
\(DF_{(t_i,t_j)}^{financing}\) (equivalent to \(DF_{(t_i,t_j)}^{repo}\)) is the discount factor associated with the combination of the risk free rate on the period and the repo spread on the period (with the repo spread almost always negative - ie positive quotation as the quotation for repo is inverted).
Implied repo
Implied repo can be easily obtained if different market values are known:
- The risk free rate curve and the associated discount factors,
- The spot and forward values of \(B\).
Ressources:
See: