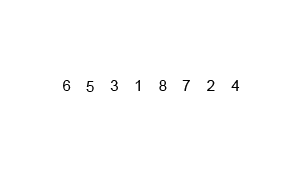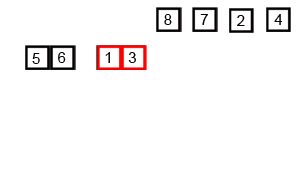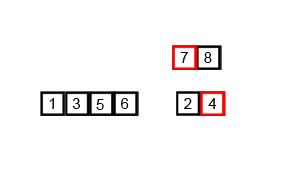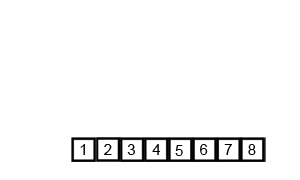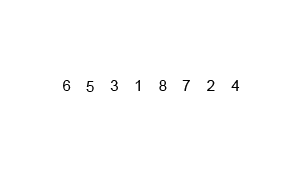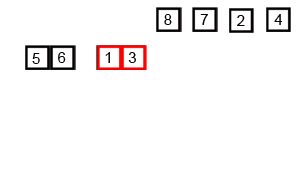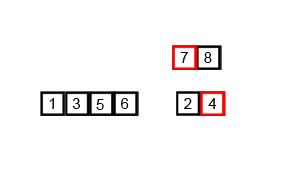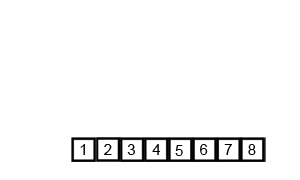Merge Sort

Merge Sort is a sorting algorithm based on the divide and conquer logic.

The algorithm will:

1) Split the array in two equal part

2) Sort each part separately

3) Merge the two sorted arrays into one new sorted array

The algorithm is called recursively with the exit case being when the splitted arrays are of length 1.

The 3rd part 'Merging and Sorting' is done in linear complexity and is called log2(n) times.

Temporal complexity: nlog(n)

Animation from Wikipedia showing the algorithm

Implementation

def merge_sort(l):
    # Exit case: a list with a single element is sorted
    if len(l) == 1:
        return(l)
    # divide the list in 2, sort each list and then merge them (in a way the result is sorted)
    return(merge(merge_sort(l[:int(len(l)/2)]), merge_sort(l[int(len(l)/2):])))
    
def merge(l1, l2):
    # l1 and l2 are sorted
    l3, i, j = [0 for _ in range(len(l1)+len(l2))], 0, 0
    
    while i < len(l1) or j < len(l2):
        # add the smallest between l1[i] and l2[j] and increment its index (beware of size limits)
        if i == len(l1) or (j < len(l2) and l1[i] > l2[j]):
            l3[i+j] = l2[j]
            j += 1
        else:
            l3[i+j] = l1[i]
            i += 1
    return(l3)

merge_sort([1, 2, 6, 5, 9, 2])

[1, 2, 2, 5, 6, 9]