A set is a collection of object that can represent mathematical objects or not.
There is no formal or mathematical definition of sets but set theory, a branch of mathematical logic, defines the properties of sets by axioms.
Different notations exist to define a set.
\(A = \{4, 2, 1, 3 \}\\\)
\(B = \{blue, white, red \}\\\)
\(C = \{1, 2, 3, ..., 1000 \}\\\)
\(D = \{0, 1, 2, 3, 4, ... \}\)
\(E = \{..., −3, −2, −1, 0, 1, 2, 3, ... \}\)
Let F be the set whose members are the first four positive integers.
Let G be the set of colors of the French flag.
\(H = \{n\mid n{\text{ is an integer, and }}0\leq n\leq 19\}\)
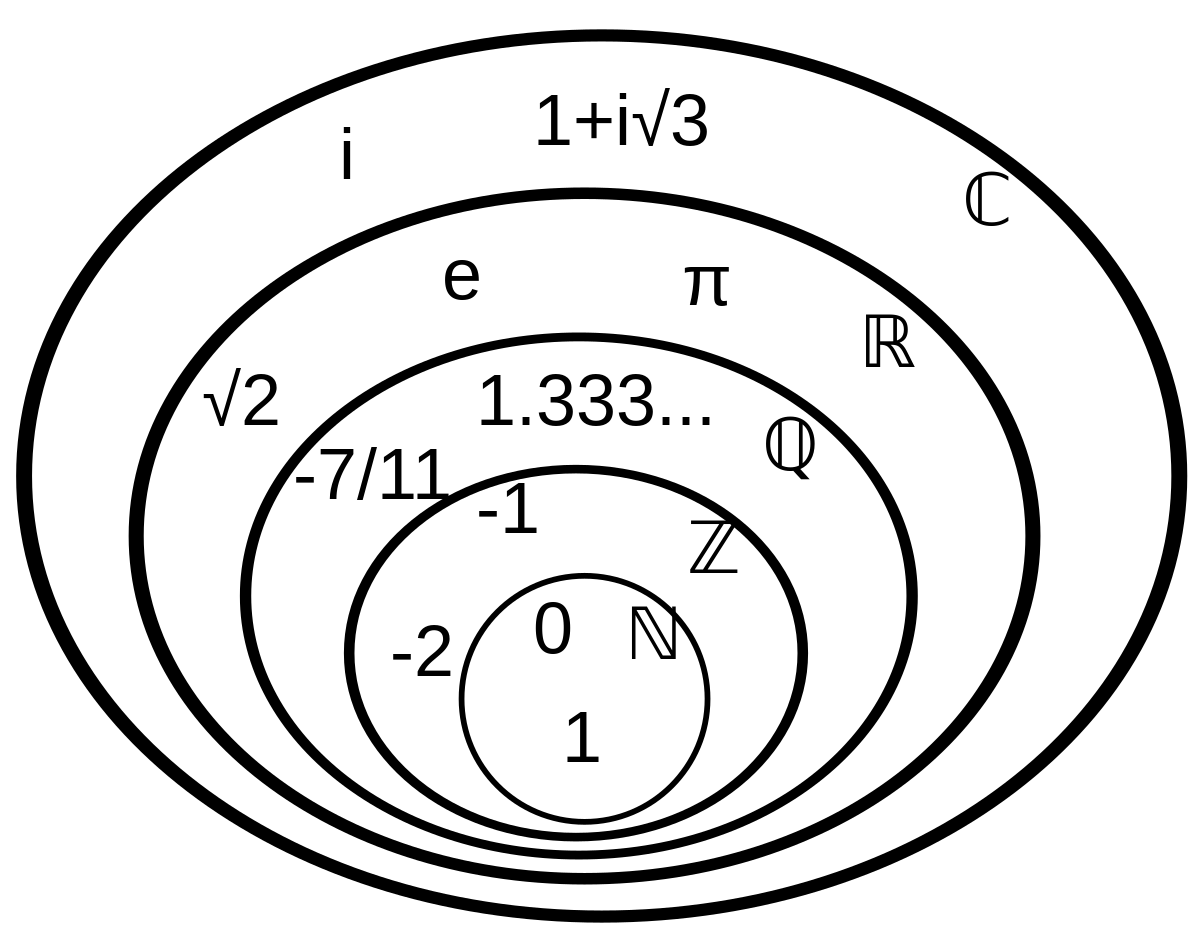
The numeric families are famous set \(\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}, \mathbb{C}\):

See:
The power set of a set \(X\) is the set of all subsets of \(X\), including the empty set and \(X\) itself.
If \(X=\{x, y, z\}\) then the power set \(\mathcal{P}(X)\) is:
\[\mathcal{P}(S) = \{\{\}, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\}, \{x, y, z\}\}\]A \(\sigma\text{-algebra}\) (tribu in french) on a set \(X\) is a nonempty (contains null element) collection \(\Sigma\) of subsets of \(X\) that contains the empty set, closed under complement, countable unions, and countable intersections.
Let \(X\) be some set, and let \(\mathcal{P}(X)\) represent its power set. Then a subset
See: