Taylor series of a function is an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. The Taylor series of a real or complex-valued function \(f(x)\) that is infinitely differentiable at a real or complex number \(a\) is the power series:
\[f(a)+\frac{f^{'}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ ...\]See: Taylor series on Wikipedia.
Taylor theorem is used to approximate a \(k\)-times differentiable function \(f(x)\) around a given point \(x\) by a polynomial of degree \(k\). For a smooth function, the Taylor polynomial is the Taylor series of the function considered for the \(k\)-th first elements.
The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is the quadratic approximation.
Let \(f(x)\) be a \(k\)-times differentiable function on point \(a\), then for an \(x\) in the neighbourhood of \(a\):
\[\begin{eqnarray} f(x) &&= f(a)+\frac{f^{'}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2 + ... + \frac{f^{(k)}(a)}{k!}(x-a)^k + o((x-a)^k) \\ &&= \sum_{i=0}^{k}\left[\frac{f^{(i)}(a)}{i!}(x-a)^i\right] + o((x-a)^k) \end{eqnarray}\]It can be rewrite using \(h\) close to \(0\) as:
\[\begin{eqnarray} f(a+h) &&= f(a)+\frac{f^{'}(a)}{1!}h+\frac{f^{(2)}(a)}{2!}h^2 + ... + \frac{f^{(k)}(a)}{k!}h^k + o(h^k) \\ &&= \sum_{i=0}^{k}\left[\frac{f^{(i)}(a)}{i!}h^i\right] + o(h^k) \end{eqnarray}\]If \(f(x)\) is \(k\)-times differentiable at point \(0\) then:
\[\begin{eqnarray} f(x) &&= f(0)+\frac{f^{'}(0)}{1!}x+\frac{f^{(2)}(0)}{2!}x^2 + ... + \frac{f^{(k)}(0)}{k!}x^k + o(x^k) \\ &&= \sum_{i=0}^{k}\left[\frac{f^{(i)}(0)}{i!}x^i\right] + o(x^k) \end{eqnarray}\]See:
Jensen’s inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation.
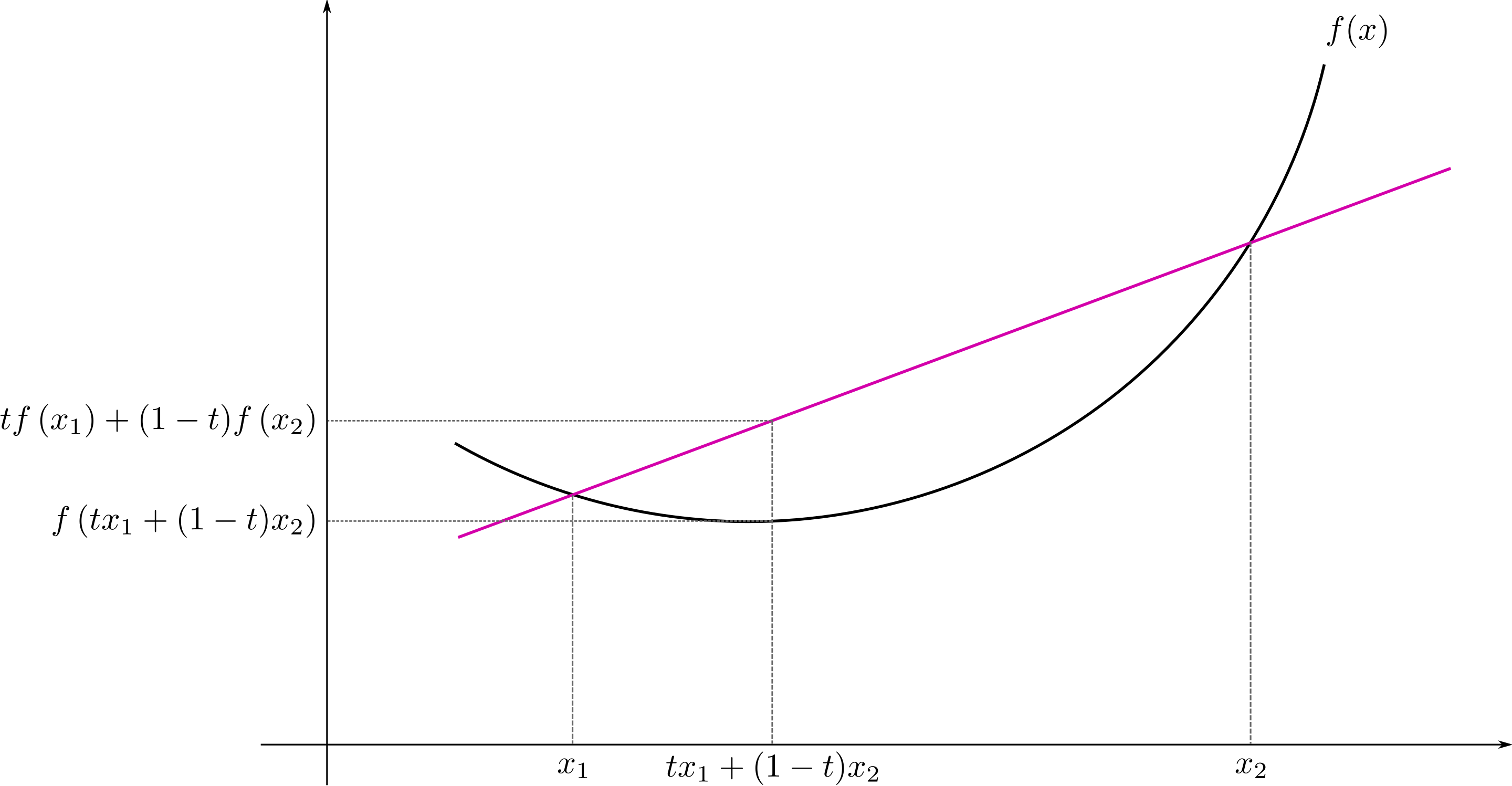
Jensen’s inequality states that for a convex function \(f\), the secant line joining two points of the function graph is above the function graph.
From a mathematical point of view, the function \(f\) applied to the weighted mean of two points \(a\) and \(b\) \(f(ta + (1-t)b)\) is smaller or equal than the weighted mean of the function applied to these two points \(a\) and \(b\) \(tf(a) + (1-t)f(b)\):
\[f(ta + (1-t)b) \leq tf(a) + (1-t)f(b)\]
Jensen’s inequality states that for a concav function \(f\), the secant line joining two points of the function graph is below the function graph.
From a mathematical point of view, the function \(f\) applied to the weighted mean of two points \(a\) and \(b\) \(f(ta + (1-t)b)\) is greater or equal than the weighted mean of the function applied to these two points \(a\) and \(b\) \(tf(a) + (1-t)f(b)\):
\[f(ta + (1-t)b) \geq tf(a) + (1-t)f(b)\]It can be directly applied to expected value of a convex function \(\phi\):
\[\varphi(\mathbb{E}[X]) \leq \mathbb{E}[\varphi(X)]\]For a function \(\phi\) concave we have:
\[\varphi(\mathbb{E}[X]) \geq \mathbb{E}[\varphi(X)]\]The finite form of Jensen’s inequality is, for a convex function \(f\):
\[\varphi \left(\frac {\sum a_{i}x_{i}} {\sum a_{i}}\right) \leq \frac {\sum (a_{i}\varphi (x_{i}))}{\sum a_{i}}\]For a concave function we have:
\[\varphi \left(\frac {\sum a_{i}x_{i}} {\sum a_{i}}\right) \geq \frac {\sum (a_{i}\varphi (x_{i}))}{\sum a_{i}}\]See: