Regularization is an ensemble of method to prevent overfitting of a model. It increases biase but decrease variance (see Bias variance tradeoff).
\(L_1\) regularization adds a norm 1 (manhattan norm) penalty to the loss ie \(\lambda \Vert W \Vert_1 = \lambda \vert W \vert\) ie:
\[C_{L_1} = C + \lambda \vert W \vert\]Similarely to the Lasso regularization in Linear Regression, the \(L_1\) penalty in neural network performs a weight selections ie it pushes some weights to 0.
\(L_2\) regularization adds a norm 1 (manhattan norm) penalty to the loss ie \(\frac{1}{2} \lambda \Vert W \Vert_2^2 = \frac{1}{2} \lambda W^2\) ie:
\[C_{L_2} = C + \frac{1}{2} \lambda W^2\]When computing the derivative of the loss for each weight \(W\) (each weight of each layer) we add in the update rule \(- \lambda W\) ie the classic gradient descent update rule would become:
\[W = W - \alpha \nabla_W - \lambda W\]It is also possible to add a constraint on the maximum norm of a weights such that:
\[\Vert W \Vert_2^2 \lt c\]Where:
It avoids the network to explode even when the gradients are really high.
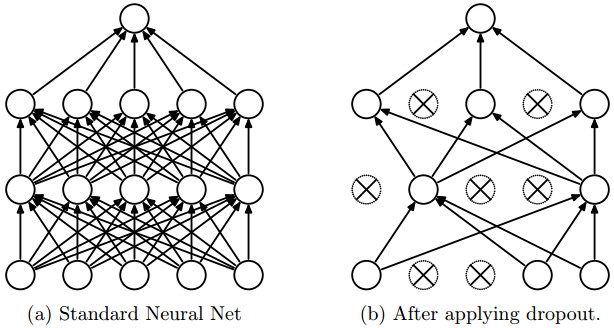
Dropout is another regularization method that can be used in complement of other methods.
During training, dropout randomly set a given percentage of weights to 0 (the percentage being an hyperparameter - generally 30%).
During testing time every weights are used. Dropout has the effect of performing a sort of ensemble of different models (each iteration with some weights set to 0 can be see as alternative model).

Figure taken from the Dropout paper that illustrates the idea. During training, Dropout can be interpreted as sampling a Neural Network within the full Neural Network, and only updating the parameters of the sampled network based on the input data. (However, the exponential number of possible sampled networks are not independent because they share the parameters.) During testing there is no dropout applied, with the interpretation of evaluating an averaged prediction across the exponentially-sized ensemble of all sub-networks (more about ensembles in the next section).