
Artificial neural networks (ANNs), usually simply called neural networks (NNs), are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives a signal then processes it and can signal neurons connected to it. The “signal” at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called edges. Neurons and edges typically have a weight that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, neurons are aggregated into layers. Different layers may perform different transformations on their inputs. Signals travel from the first layer (the input layer), to the last layer (the output layer), possibly after traversing the layers multiple times.
NN can be used for regression or classification. It is widely used for complex tasks such as natural language processing (NLP), computer vision or deep reinforcement learning.
Deep learning is a branch of learning based on ANN with a lot of parameters (a lot of layers, the depth).
See Wikipedia page on Artifical Neural Network.
A neural network is a serie of layers, each layers being composed of neurons.
The input data (green dots) is connected to the first layer of neurons (blue dots) by the weights (black arrows). Then these neurons are transfered to the next layer by other weigths until getting to the output (purple dot).
Here is an image of a very shallow network. The arrows represent the weights:

From Wikipedia’s Neural Network page. The hiden layer is composed of units that are called neurons.
Here is more in details how a neuron is created from the weights and the input data.
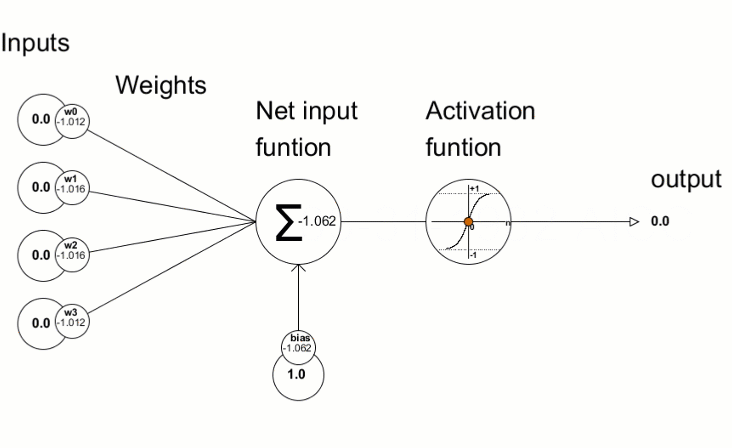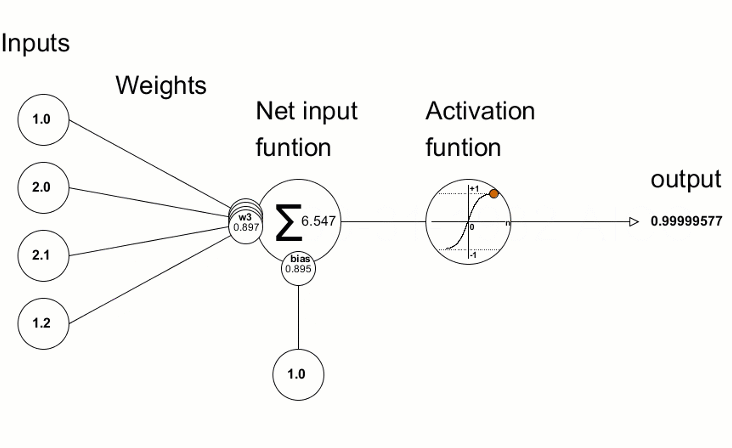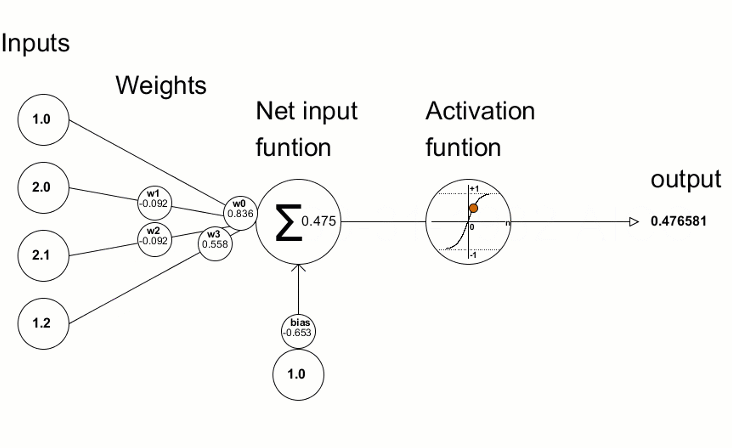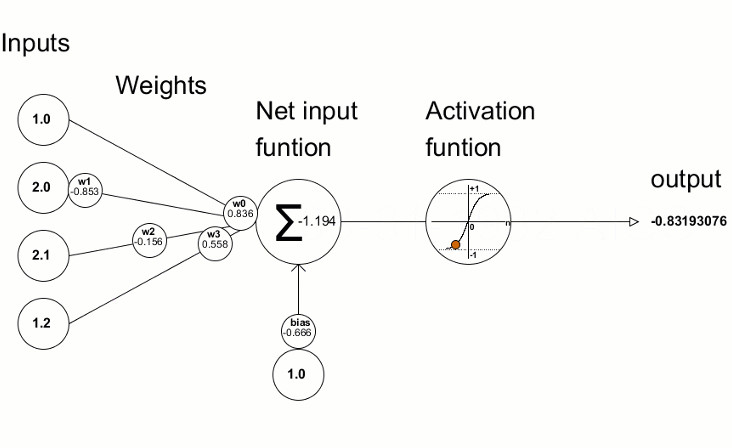
From https://www.mql5.com/fr/articles/5486. In this second scheme, the output is the output of the neuron, ie its value (not the output of the network).
The activation function that we see in this scheme is an important part of a neural network.
The formula of a neural network can be written as follow:
\[\begin{eqnarray} Y &&= \underset{l=1}{\stackrel{L}{\circ}} f\left(\sum_{i=1}^{n_{weights}} W_i^l x_i^l + b^l\right) \\ &&=\underset{l=1}{\stackrel{L}{\circ}} f\left(W^l x^l + b^l\right) \end{eqnarray}\]Where:
It can also be rewrite:
\[Y = f^L \left(b^L + W^L f^{L-1}\left(b^{L-1} + W^{L-1} \cdots f^{1}(b^1 + W^1 x) \cdots \right)\right)\]Note that \(x^l=f^{l-1}(b^{l-1} + W^{l-1}x^{l-1})\).
A neural network with a single hidden layer with unlimited number of neurons can approximate any function. The idea of the proof is to show that we can create step functions with a single neuron and that we can add step functions with different neurons.