Vanishing gradient is a problem that appears when the gradient of the neural network is too small and the parameters of the network (the weights) have very small updates. In this case the training will be stuck in an area as the updates are too slow.
The two main causes of vanishing gradient are:
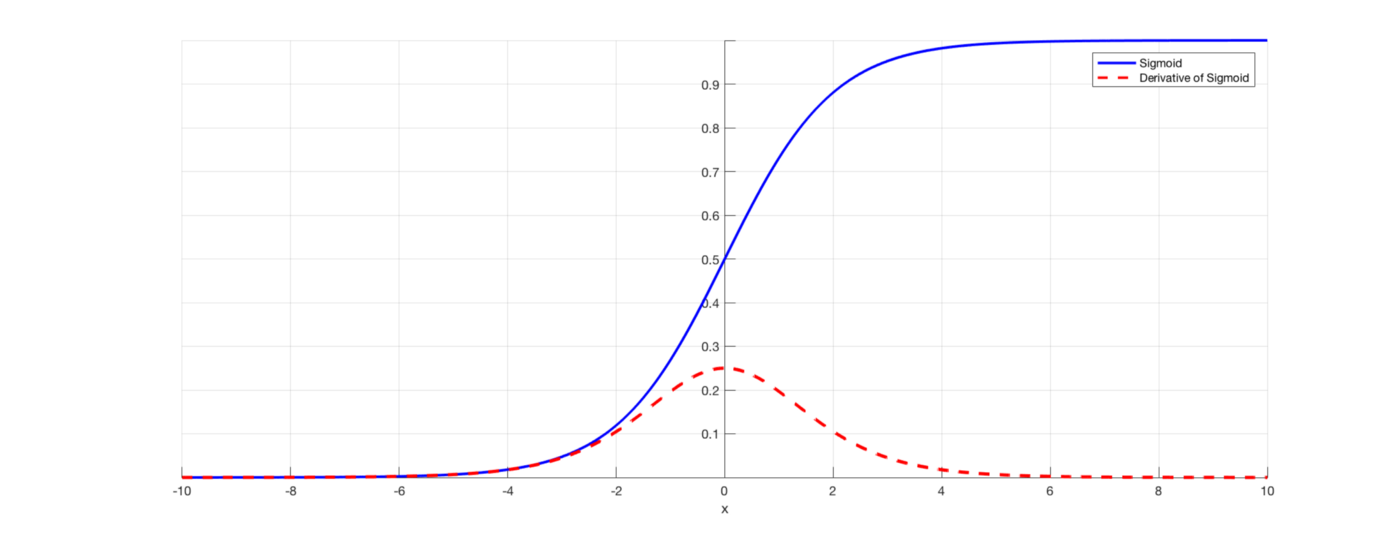
As said previously, activation functions that squishe large input space in a small output space are prone to vanishing gradient as the gardient for input data far from 0 are very close to 0:

Hence each time the network as an activation function like sigmoid or tan, the gradient has a probability to become very small.
For large network this probability converges to 1.
The solutions are of two kinds.
Activation function like ReLU, Leaky ReLU or ELU and its derivatives are not prone to vanishing gradient as they do not squishe large input space in a small output space.
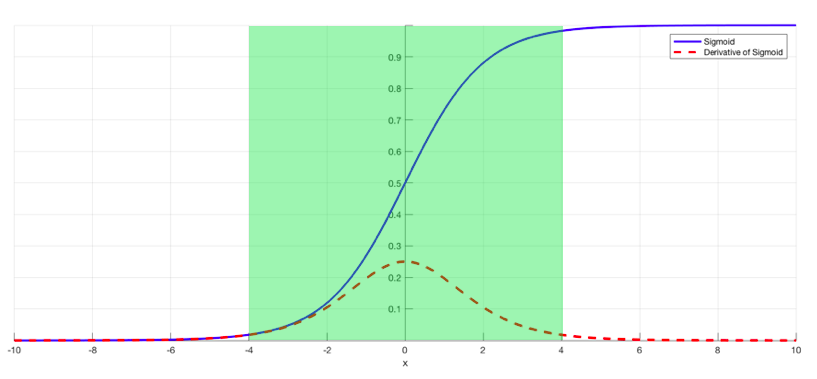
A proper initialization coupled with Batch normalization is another solution when using sigmoid or tan activation function. Indeed, they will insure the output of a layer to have a distribution \(\mathcal{N}(0, 1)\) hence the derivative of sigmoid (or tan) won’t be vanished:
Even with a the problem due to the activation function fix, a deep neural network can be prone to vanishing gradient due to its depth (it is also prone to exploding gradient).
Indeed, the product of n numbers has an high probability to vanish or explode when n converge to infinity.
The solution is to use residual block.
A residual block adds the value of a layer to a layer further in the network. As the derivative of an addition will just transfer the current gradient (without multiplying it), the flow of gradient won’t vanish (or explode).

A residual block just add the input of a layer to its output (or to the output of a layer further).
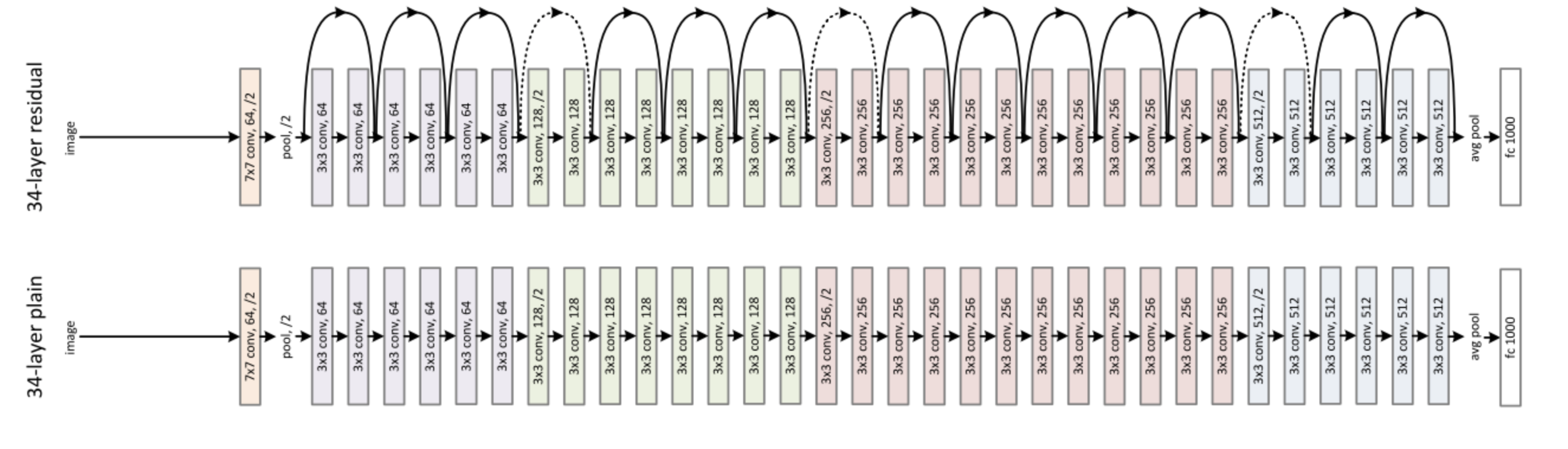
The black arrows represent residual block where the output of a layer is added to the output two layers further.
See:
Exploding gradient is the opposite of vanishing gradient. It appears also in neural network and more probably in deep networks.
Exploding gradient make updates to the parameters that are to important.
Same as vanishing gradient, a proper initialization and batch normalization will insure the output of a layer to have a distribution \(\mathcal{N}(0, 1)\) and hence it will prevent the model to generate large outputs of layers and hence it prevents exploding gradient.
Another popular method is gradient clipping that will clip the gradient value between to chosen values. For example it is possible to clip the gradient between \(-1\) and \(1\). This will hence prevent exploding gradient.
See: